Объяснение:
Построить график функции
у=2×|х|+3
Шаг 1.
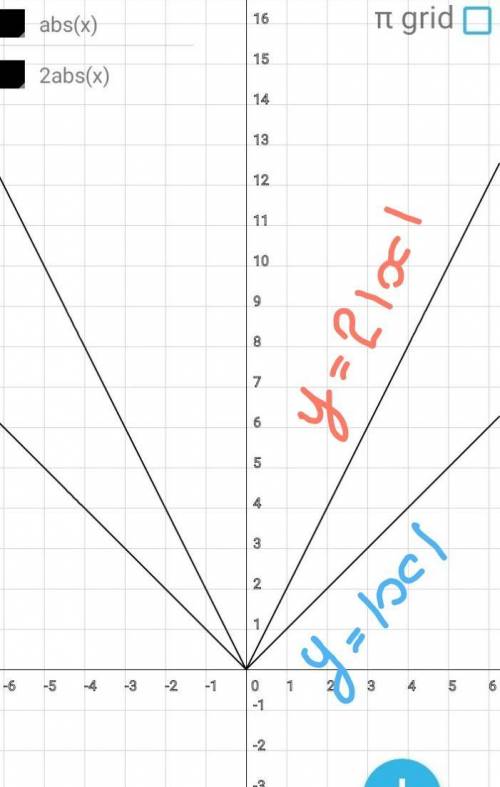
Строим график функции
у=|х|
Графиком являются биссектрисы
1 и 2 координатных четвертей.
Весь график расположен в верхней
полуплоскости.
Шаг 2.
Нужно изменить угол наклона вет
вей графика.
Построим и заполним таблицу:
у=2×|х|
х 0 -2 2
у 0 4 4
Строим график фунеции
у=2×|х|.
Шаг 3.
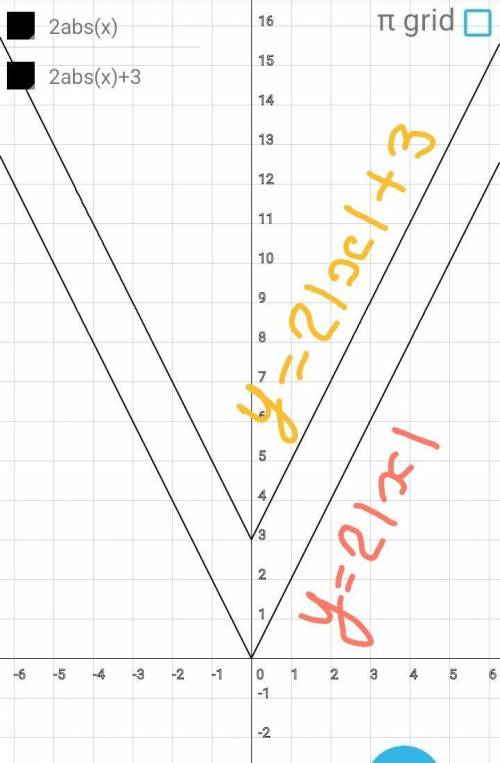
Строим график функции
у=2×|х|+3
График функции у=2×|х| поднимаем
вверх на 3 единицы ( совершаем па
раллельный перенос вдоль положи
тельного направления ОУ на 3ед. от
резка).
Построен искомый график.
Допустим, что 
. Тогда имеем уравнение 
, не имеющее решений, поскольку в левой части число неположительное, а в правой - положительное, т.е. левая часть никак не может быть равна правой. Т.е.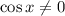 
Преобразуем правую часть:
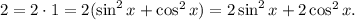
Перенесем все влево с противоположным знаком:
Поскольку 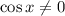, можем разделить обе части уравнения на 
. В итоге имеет равносильное исходному уравнение
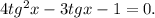
Заметим, что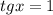 
является корнем уравнения относительно тангенса. Тогда по теореме Виета второй корень равен 
.
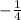Соответственно, имеем два случая: или 
или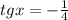 
.
1 случай.
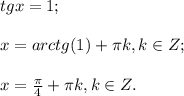
2 случай.
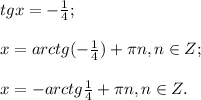
Имеем две серии корней.
ОТВЕТ: π/4 + πk, k ∈ Z; -arctg(1/4) + πn, n ∈ Z.
если x<0, а арифметический квадратный корень из положительного числа положителен, то неравенство верно при любом х <0
Решением первого случая является (-∞;0)
если х≥0, то возводим обе части в квадрат
х²+7≥х²
7≥0- верно при любом х≥0
О т в е т. х∈(-∞;0)U[0;+∞)=(-∞:+∞)
б) -1≤ cosx ≤1
cosx < - √3 -неравенство не имеет решений