Question

Объясните, как происходит умножение таких чисел как, например, , заранее : )

Answer 1

Первый

1)используем правило

$a {}^{ - x}=\frac{1}{a {}^{x} }$,значит

$10 {}^{ - 11}=\frac{1}{10 {}^{11} }$

2)сокращаем и умножаем:

$6.7* \frac{1}{10 {}^{11} } *0.6*10^{3}=\frac{6.7 \times 0.6 \times 10 {}^{3} }{10 {}^{11} }=\frac{4.02}{10 {}^{8} }= 4.02 \times 10 {}^{ - 8}$

Второй быстрее)

1)меняем местами множители и используем правило:

$a {}^{x}\times a {}^{y}= a {}^{x + y}$,получим

$6.7*10^{-11}*0.6*10^{3} = 6.7 \times 0.6 \times 10 {}^{ - 11}\times 10 {}^{3}=4.02 \times 10 {}^{ - 11 + 3}= 4.02 \times 10 {}^{ - 8}$

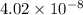($4.02 \times 10 {}^{ - 8}$-стандартный вид числа 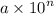$a\times {10}^{n}$, где 1≤а<10 и n (натуральное или целое число)

Answer 2

Очень просто

Объяснение:

Сначала мы умножаем 10-ки. При умножении складываем их степени. В данном случае 10⁻¹¹*10³=10⁻¹¹⁺³=10⁻⁸. Далее умножаем 6.7 и 0.6.

6.7*0.6=4.02

в итоге получаем 4.02*10⁻⁸.