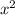Объяснение:
преобразовывая первое уравнение получаем:
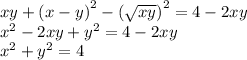
при условии xy>0
из второго уравнения:
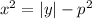
a)
при y>=0
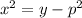
подставляем
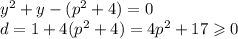
при всех p дискриминант будет больше 0, поэтому решение квадратного уравнения будет при всех p.
уравнение не имеет решений только в том случае если корни уравнения будут y<0
это значит, что:
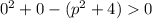
ни при каких p не будет соблюдаться неравенство
b)
при y<0
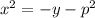
подставляем
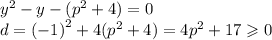
при всех p дискриминант больше нуля, поэтому уравнение имеет решение при всех p.
уравнение не имеет решений только в том случае если корни уравнения будут y>0
это значит, что:
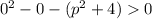
ни при каких p не будет соблюдаться неравенство.
Поэтому можно сделать вывод, что при любых p система будет иметь решение.
+bx+c если знаешь x и y?
1.
Вероятность рассчитывается как отношение благоприятных исходов к общему числу исходов.
Поскольку в мешке А 3 белых шара, а общее число шаров 3+2=5, то вероятность достать белый шар из мешка А:
Поскольку в мешке В 3 белых шара, а общее число шаров 3+4=7, то вероятность достать белый шар из мешка В:
Так как вероятность достать белые шары из мешков А и В независимы, то достать белые шары и из мешка А и из мешка В равна произведению двух ранее найденных вероятностей:
2.
Поскольку в мешке В 4 белых шара, а общее число шаров 3+4=7, то вероятность достать черный шар из мешка В:
Предположим, что после первой попытки из мешка В достали черный шар. Тогда, черных шаров в нем осталось 3, а общее число шаров в нем стало 6. Вероятность достать следующий черный шар:
Поскольку второе событие осуществимо только при условии наступления первого, то вероятность достать два черных шара подряд равна произведению двух вероятностей: