Объяснение:
Уравнение вида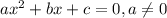 
называется квадратным уравнением.
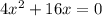
а) Если один из коэффициентов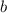 
или с равен нулю, то уравнение называется неполным . Данное уравнение неполное квадратное уравнение.
б) старший коэффициент а= 4;
второй коэффициент b= 16;
свободный член с= 0
в) решим данное уравнение. Для этого вынесем 4х ха скобки и разложим левую часть уравнения на множители.
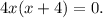
Произведение равно нулю, если хотя бы один из множителей равен нулю, а другой при этом определен
х=0 или х+4=0
х= - 4
Данное уравнение имеет два корня - 4 и 0 .
у=х-4 и y=x+3, графики этих функций параллельны, а система этих уравнений не имеет решений.
Объяснение:
К данному уравнению x−y=4 выбери из предложенных уравнений второе уравнение так, чтобы полученная система не имела решений:
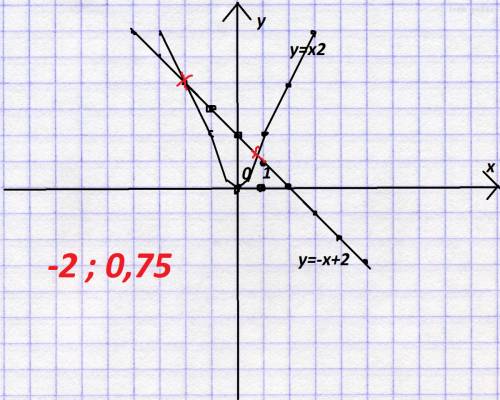
ответ (можно получить, используя построение):
2x−y=5
y+x=−4
y=x+3
Можно не использовать построение, а ответ получить, опираясь на знания)
Для начала все уравнения запишем в виде уравнений функций:
x−y=4 2x−y=5 y+x=−4 y=x+3
-у=4-х -у=5-2х у= -4-х
у=х-4 у=2х-5 у= -х-4
Известно, что система не имеет решений, если графики функций, выраженных этими уравнениями, параллельны.
Известно также, что графики линейных функций параллельны при одинаковых коэффициентах при х.
Смотрим на коэффициенты при х.
у=х-4 и y=x+3, графики этих функций параллельны, а система этих уравнений не имеет решений.
