x ∈ [⅔; 6)
Объяснение:
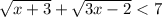
ОДЗ:
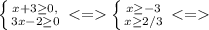 x ∈ [⅔; +∞)
x ∈ [⅔; +∞)
Возводим в квадрат обе части уравнения:
(√(x + 3) + √(3x - 2))² < 7²
Решаем:
x + 3 + 2√((x + 3)(3x-2)) + 3x - 2 < 49
4x + 1 + 2√(3x² + 7x - 6) < 49
2√(3x² + 7x - 6) < 48 - 4х | :2
√(3x² + 7x - 6) < 24 - 2x
Имеем два случая:
Если 1) 24 - 2x < 0, то нет корней;
2) 24 - 2x ≥ 0
(√(3x² + 7x - 6))² < (24 - 2x)² при 24 - 2x ≥ 0
ОДЗ: 3x² + 7x - 6 ≥ 0; (x+3)*(3x - 2) ≥ 0
+ - +
------•------•------>
-3 ⅔
ОДЗ: x ∈ (-∞; -3] ∪ [⅔; +∞)
Решаем далее:
3x² + 7x - 6 < 4x² - 96x + 576
-x² + 103x - 582 < 0
(x - 6)*(x - 97) > 0 *корни уравнения x² - 103x + 582 = 0 были найдены по т-ме Виета
+ - +
------о------о------>
6 97
х ∈ (-∞; 6) ∪ (97; +∞)
Так как мы взяли 24 - 2х ≥ 0, то: 24 ≥ 2x; x ≤ 12.
х ∈ (-∞; 6) ∪ (97; +∞) при x ≤ 12, то у нас решение первого нер-ва: х ∈ (-∞; 6).
В итоге, решением заданного по условию неравенства является решение 1-го полученного неравенства и ограничения начального неравенства:
х ∈ (-∞; 6) при x ∈ [⅔; +∞)
Пересечением данных неравенств является интервал: x ∈ [⅔; 6). Это и будет ответом.
сумма корней квадратного трехчлена равна его второму коэффициенту с противоположным знаком, а произведение - свободному члену .
в случае квадратного уравнения формулы виета имеют вид:
значимость теоремы виета заключается в том, что, не зная корней квадратного трехчлена, мы легко можем вычислить их сумму и произведение, то есть простейшие симметричные многочлены от двух переменных и . теорема виета позволяет угадывать целые корни квадратного трехчлена.
. используя теорему виета, найти корни уравнения
решение. согласно теореме виета, имеем, что
подбираем значения и , которые удовлетворяют этим равенствам. легко видеть, что им удовлетворяют значения
и
ответ. корни уравнения ,
обратная теорема виета
если числа и удовлетворяют соотношениям , то они удовлетворяют квадратному уравнению , то есть являются его корнями.
. зная, что числа и - корни некоторого квадратного уравнения, составить само это уравнение.
решение. пусть искомое квадратное уравнение имеет вид:
тогда, согласно теореме виета, его коэффициенты связаны с корнями следующими соотношениями:
тогда
то есть искомое уравнение
ответ.
общая формулировка теоремы виета
если - корни многочлена (каждый корень взят соответствующее его кратности число раз), то коэффициенты выражаются в виде симметрических многочленов от корней, а именно:
иначе говоря, произведение равно сумме всех возможных произведений из корней.
б) там идёт минус