:
(С ФСУ)
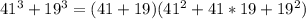
Выражение делится на число тогда, когда один из множителей делится на число
41 + 19 = 60, 60 делится на 60, следовательно и сумма будет делится
:
(Более замороченный)
Для этого можно просто доказать кратность этого выражения на множители числа 60.
60 =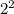 
* 3 * 5
41, при делении на 5, дает остаток 1 (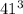
так же будет давать этот остаток)
19, при делении на 5, дает остаток 4 (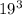
так же будет давать этот остаток)
1 + 4 = 5 : 5
Сумма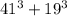 
будет делится на 4 ( по признаку деления на 4, сумма будет оканчиваться на 0)
А деление на 3 можно доказать суммой цифр, 4+1 = 5 (остаток, при делении на 3, 2), 1 + 9 = 10 (остаток, при делении на 3, 1)
1 + 2 = 3 : 3
чтд
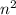коэффициент положительный, ветви параболы смотрят вверх, следовательно больше нуля заштрихованная область.
2a(a^2+b^2)-a(a-b)^2+a(b+a)^2-2a^3 =
2a³ + 2b³ - a*(a² - 2ab + b²) + a*(a² + 2ab + b²) - 2a³ =
= 2b³ - a³ + 2a²b - ab² + a³ + 2a³b + ab² - 2a³ =
= - 2a³ + 4a²b + 2b³