task/30683252 Найдите площадь фигуры | x - 5 | + | y + 9 | ≤ 4
решение рис. см ПРИЛОЖЕНИЕ
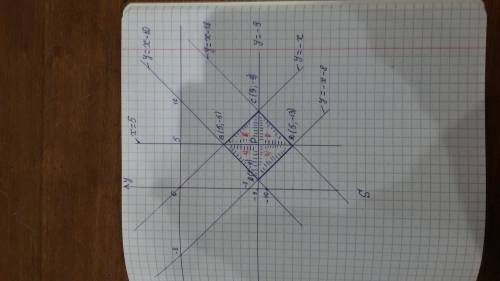
a) { x - 5 < 0 ; y + 9 ≥ 0 ; -(x - 5) + y + 9 ≤ 4. ⇔ { x< 5 ; y ≥ - 9 ; y ≤ x -10 . Δ ABP
б) { x - 5 ≥ 0 ; y + 9 ≥ 0 ; x - 5 + y + 9 ≤ 4. ⇔ { x≥ 5 ; y ≥ - 9 ; y ≤ - x . Δ BCP
в) { x - 5 ≥ 0 ; y + 9 < 0 ; x - 5 - (y + 9) ≤ 4. ⇔ { x ≥ 5 ; y <- 9 ; y ≥ x -18 . Δ СDP
г) { x - 5 < 0 ; y + 9 < 0 ; -(x - 5) - (y + 9) ≤ 4. ⇔{ x < 5 ; y <- 9 ; y ≥ - x - 8 . Δ DAP
A( 1; -9) , B(5; -5) , C(9; -9) , D(5; -13) AB || CD ; BC || AD ; AB⊥ BC
ABCD квадрат S =AC²/2 = 8²/2 =32 кв. единиц
ответ: 32 кв. единиц
2на3 если не правильно пиши