Відповідь:
a ≥ -1
Пояснення:
Спочатку розв'яжемо подвійну нерівність. Розглянемо два можливих випадки під час розкриття модуля.
Перший: вираз під знаком модуля невід'ємний.
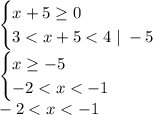
Другий: вираз під знаком модуля від'ємний
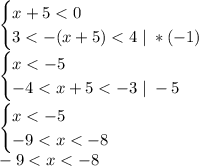
Отже, множина розв'язків цієї нерівності
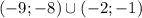
Виразимо x із нерівності з параметром:
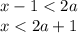
Видно, що всі розв'язки подвійної нерівності менші за -1. Тобто якщо вираз (2a+1) буде не меншим за -1, то він буде більшим і за кожний розв'язок подвійної нерівності. Інакше кажучи, підставивши замість x розв'язок нерівності 3<|x+5|<4 у нерівність x<2a+1, де 2a+1 ≥ -1 (конкретне значення), отримаємо правильне твердження. А це задовольнить умову задачі.
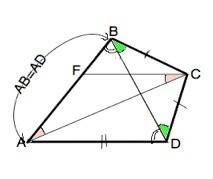
Проведем в данном четырехугольнике диагональ BD.
По услоию AF=FC, BC=CD, AB=AD ⇒
∆ АВD и ∆ ВСD - равнобедренные.
Рассмотрим треугольники АВС и АDС. Они равны по трем сторонам ( две по условию, сторона АС - общая)
Следовательно, ∠ВАС=∠DАС, ⇒ АС - биссектриса угла ВАD
В ∆ АFC стороны AF=CF, ∆ AFC – равнобедренный, ⇒ ∠FAC=∠FCA.
Но ∠ВАС=∠САD (из доказанного равенства ∆ АВС и ∆ АDС).
Из этого следует ∠FCA=∠CAD, а эти углы - накрестлежащие при пересечении FC и AD секущей АС.
Если при пересечении двух прямых третьей секущей накрест лежащие углы равны, то эти прямые параллельны. ⇒
FC||AD. Доказано.
4x в квадрате -11x -3=0
3-x не равно нулю,потому что в знаменателе никогда не должен быть ноль,на ноль делить нельзя
4x в квадрате-11x-3=0 решаем через дискриминант
Д=121-4*(-3)*4
Д=169, Д>0,2 корня
x=11-13/8=-0.25
x=11+13/8=3 является посторонним корнем,так как если мы поставим вместо x в знаменателе 3 то получится ноль,а на ноль делить нельзя
корень x=-0.25