1)31 (км/час) скорость лодки в стоячей воде.
2)54,4 (км) до места встречи пройдёт лодка, плывущая по течению.
3)44,8 (км) до места встречи пройдёт лодка, плывущая против течения.
Объяснение:
Расстояние между двумя пристанями равно 99,2 км. Из них одновременно навстречу друг другу вышли две лодки, скорости которых в стоячей воде равны. Через 1,6 ч. лодки встретились. Скорость течения реки равна 3 км/ч.
1)Скорость лодки в стоячей воде?
2)Сколько километров до места встречи пройдёт лодка, плывущая по течению?
3)Сколько километров до места встречи пройдёт лодка, плывущая против течения?
х - скорость лодки в стоячей воде
х+3 - скорость лодки по течению
х-3 - скорость лодки против течения
Формула движения: S=v*t
S - расстояние v - скорость t - время
Согласно условию задачи составляем уравнение:
(х+3)*1,6+(х-3)*1,6=99,2
Разделим уравнение на 1,6 для упрощения:
(х+3)+(х-3)=62
Раскроем скобки:
х+3+х-3=62
2х=62
х=31 (км/час) скорость лодки в стоячей воде.
(31+3)*1,6=54,4 (км) до места встречи пройдёт лодка, плывущая по течению.
(31-3)*1,6=44,8 (км) до места встречи пройдёт лодка, плывущая против течения.
Чтобы оценить периметр исходного треугольника, нужно сложить заданные неравенства
2,3 ≤ a ≤ 2,4
3,2 ≤ в ≤ 3,3
4,5 ≤ c ≤ 4,6
2,3+3,2+4,5 ≤ a+в+с ≤ 2,4+3,3+4,6
10 ≤ P ≤ 10,3
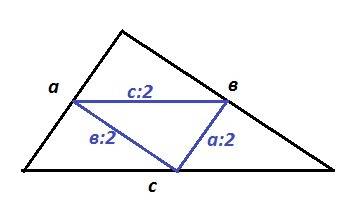
Соединили середины сторон, то есть провели 3 средние линии треугольника. Каждая средняя линия равна половине стороны, которой параллельна. Значит, периметр образованного треугольника равен половине периметра исходного треугольника
10 ≤ P ≤ 10,3 | : 2
10:2 ≤ P:2 ≤ 10,3 :2
5 ≤ P₁ ≤ 5,15
ответ : периметр полученного треугольника в пределах от 5 см до 5,15 см включительно.
(m+7)(9m+5)-m(m-2)=9m^2+5m+63m+35-m^2+2m=8m^2+70m+35 не делится на 7
1+p+q+pq= (1+p)+(q+pq)=1(1+p)+q(1+p)=(1+p)(1+q)
при p=1,012 и q=999
(1+1,012)(1+999)=2,012*1000= 2012