
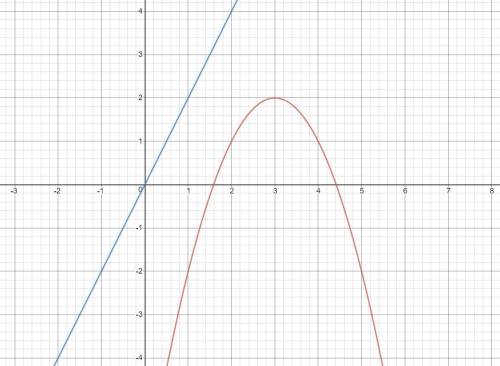
Строим графики функций. y=-x²+6x-7 - парабола с ветвями вниз. y=2x+a - прямая y=2x, которая перемещается вдоль оси Oy в зависимости от значения a (картинка 1).
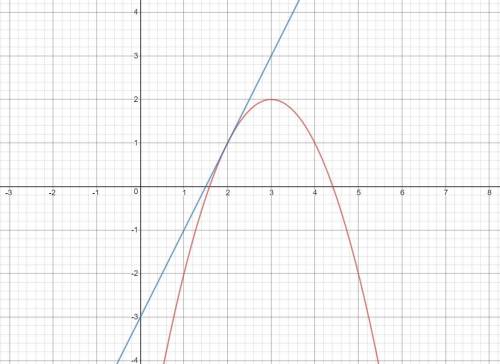
При некотором a прямая будет касательной к параболе (картинка 2). В таком случае уравнение -x²+6x-7=2x+a будет иметь один корень, что соответствует нулевому дискриминанту.
-x²+6x-7=2x+a ⇒ x²-4x+7+a=0
D=16-4(7+a)=16-28-4a=-4a-12 ; -4a-12=0 ⇒ a=-3
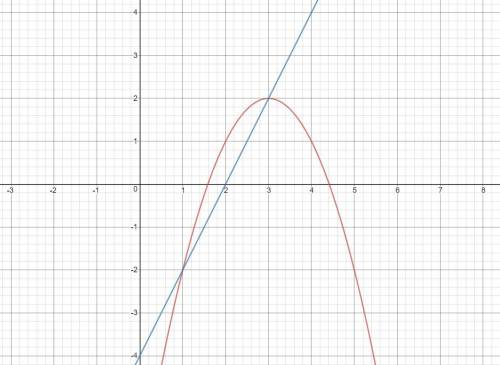
При меньших a прямая будет пересекать параболу в двух точках (картинка 3). Получим окончательный ответ a∈(-∞; -3]
ответ: a∈(-∞; -3]
S=1/3t²+3t-5
v(t) = S`(t) = - 2/3t³ + 3
a(t) = v `(t) = [(- 2/3)*t⁻³ + 3] ` = 2/t⁴
a(3) = 2/(3⁴) = 2/81