ответ. Р=36 см .
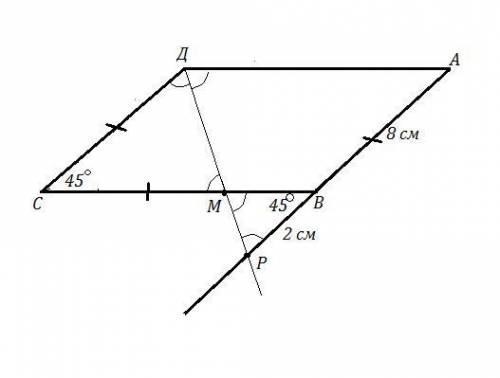
АВСД - параллелограмм , ДР - биссектриса, ∠С=45° ,
ДР пересекает АВ в точке Р , а ВС в точке М .
АР=10 см , ВР=2 см ⇒ АВ=10-2=8 см , СД=АВ=8 см как противоположные стороны параллелограмма .
ДР - биссектриса ⇒ ∠СДР=∠АДР .
∠АДР=∠СМД как накрест лежащие углы при АД || ВС и секущей ДР .
В ΔСМД два угла равны ⇒ ΔСМД - равнобедренный и СМ=СД=8 см ∠СМД=(180°-45°):2=67,5°
∠ВМР=∠СМД=67,5° как вертикальные .
В ΔВМР угол ∠МВР=45° , так как ∠МВР=∠МСД=45° как накрест лежащие углы при АР || СД и секущей ВС .
Но тогда в ΔВМР: ∠ВРМ=180°-45°-67,5°=67,5° , то есть ΔВМР есть два равных угла: ∠ВМР=∠ВРМ=67,5° , тогда этот треугольник равнобедрен-ный и ВМ=ВР=2 см .
Тогда ВС=СМ+ВМ=8 +2 =10 см , АД=ВС=10 см
Периметр Р=10+10+8+8=36 см .
х³+2х²+4х+3=х³+х²+3х+х²+х+3
х³+2х²+4х+3-х³-х²-3х-х²-х-3=0
ответ:0
2) 2x(x²-3)+x²(x+1)=2(x²+1)+2(x+1)
2х³-6х+х³+х²=2х²+2+2х+1
2х³-6х+х³+х²-2х²-2-2х-1=0
3х³-х²-8х=-3
х(х²-х-8)=-3
х=-3
х²-х-8=-3
х²-х-5=0
Д=б²-4ас=1-4*1*(-5)=1+20=21
х₁=1+√21/2
х₂=1-√21/2