Объяснение:
Заметим:
10¹ = 10 (двузначное число)
10² = 100 (трехзначное число)
10³ = 1 000 (четырехзначное число)
10⁴ = 10 000 (пятизначное число)
.............................................................
Мы можем заметить, что если степень четная, то число будет иметь нечетное число цифр...
По условию - степень четная, значит в записи числа 10²⁴ нечетное число знаков.
А теперь рассмотрим заданное число а.
a = 100...00120 ( здесь первая 1 стоит на нечетном месте)
Сумма цифр, стоящих на нечетных местах равна (1+0+... 1+0) = 2
Сумма цифр, стоящих на четных местах равна (0+0+...+2) = 2
Эти суммы РАВНЫ, значит заданное число делится на 11.
Вспомним признак делимости на 11:
Первый геометрический смысл производной)
Производная в точке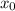 
равна угловому коэффициенту касательной к графику функции 
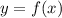в этой точке.
Пусть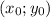 
- точка касания двух графиков. Тогда
y = -2x + 2 - касательная к графику y = -x² + p ⇒ k = -2
Производная функции: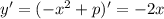 
Используя геометрический смысл производной, мы получим
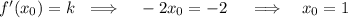
Получили абсциссу точку касания, тогда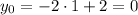 
Тогда, подставив точку (1;0) в первый график уравнения, найдем р
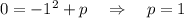
При р = 1 имеется общая точка (1;0) графика функции y = -x² + 1 и прямой y = -2x + 2.
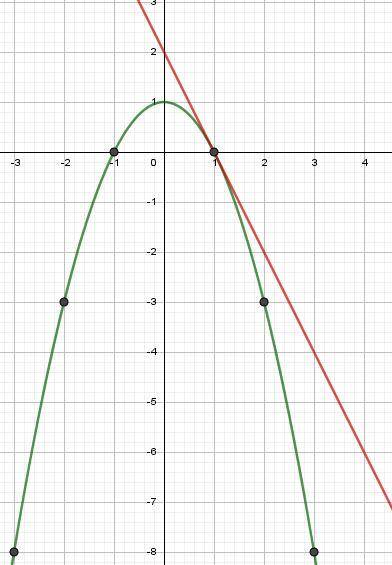
y = -x² + 1 - парабола, ветви которой направлены вниз. Вершина параболы (0;1). Точки построения изображены на картинке.
y = -2x + 2 - прямая, проходящая через точки (0;2), (1;0).
Второй Определение через дискриминант)
Приравниваем функции: -x² + p = -2x + 2 или -x² + 2x + p - 2 = 0
D = b² - 4ac = 4 + 4(p-2) = 4(1 + p -2) = 4(p-1)
Чтобы графики имели одну общую точку, достаточно чтобы квадратное уравнение имело одно единственное решение, т.е. когда D = 0.
4(p-1) = 0
p = 1.
При р = 1, получим -x² + 2x + 1 - 2 = 0 ⇔ -(x-1)² = 0 ⇒ x=1
y = -1² + 1 = 0
Координаты точки касания двух графиков (1;0).
Признак делимости на 11:
разность суммы цифр, стоящих на нечетных позициях (при нечетных степенях разложения числа), и суммы цифр, стоящих на четных позициях (при четных степенях разложения числа), должна делиться на 11.
Число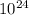
- это 1 и следом за ней 24 нуля.
Если к числу прибавить 120, получится 100...00120
То есть, на нечетных позициях стоит 1, много нулей, ещё 1, и последний 0.
А на нечетных позициях стоит много нулей и 2.
Первая сумма 1+1=2
Вторая сумма 2.
Их разность равна 2-2=0, 0 делится на 11, значит, и само исходное число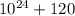
делится на 11.
P.S. про разложение - имел в виду это: