-6,7059
Объяснение:
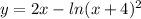
Сначала находим производную нашей функции
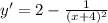
Затем приводим функцию к нулю, превратив его в уравнение
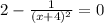
Область допустимых значений (ОДЗ) нашего уравнения ровна
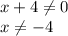
Упрощаем уравнение, домножив обе части на 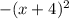
Получаем 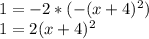
Упростим уравнение 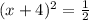
Возведем обе части под корень, чтоб избавиться от квадрата
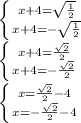
x≈ -3.29 и x≈-4.70
Делаем проверку ОДЗ
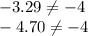
Оба выражения верны, следовательно чертим числовую прямую
\\\\\\\\\\\\\\\\\\\\\\\\\•\\\\\\\\\\\\•ххххххххх•ххххххх•////////////////////////////→
-4.70 -3.5 -3.29 0
Нам подходит только x≈-3.29
Теперь в саму функцию подставляем x
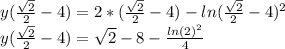
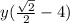 ≈
≈ 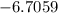
ответ: Наибольшее значение функции y=2x-ln(x+4)^2 на отрезке [-3,5;0] равно -6,7059
f(x+2)=(x+2)²=x²+4x+4
f(x+3)=(x+3)²=x²+6x+9
f(x+2)=f(x+3)
x²+4x+4=x²+6x+9
4x-6x=9-4
-2x=5
x=5:(-2)
x=-2,5