1. Вычислить A = 2㏒₂㏒₃81+㏒₉√3
решение : 2㏒₂㏒₃81+㏒₉√3 =2㏒₂㏒₃3⁴ + (1/2)㏒₃√3 = 2㏒₂4 + (1/2)*(1/2) =2*2+0,25 = 4,25 .
* * * * * * * * * * * * * * * * * * * *
Не мешает
2.Треугольник ABC имеет стороны AB = 137; AC = 241 и BC = 200. На BC есть точка D, такая, что обе окружности, вписанные в треугольники ABD и ACD, касаются AD в одной точке E. Определите длину CD .
ответ: 152
Пошаговое объяснение:
рисунок приведен во вложении Обозначаем :
DT₁ = DE= DT₂ = y и BK₁ = BT₁ = x .
Используем часть известной теоремы (дальше простоя арифметика )
Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности .
AК₂ = AE = AK₁ = AB - BK₁ = 137 - x ;
CT₂ = CK₂ =AC -AK₂ = 241 -(137 - x) = 104 + x .
- - - - - - -
BD + CD = BC BD = BT₁ + DT₁ =x + y ; CD= СT₂ +T₂D ) = 104+x+y
( x + y ) + (104 +x +y) = 200 ⇔ x + y = 48
CD =1 04+ x+y = 104+48 = 152 .
Объяснение:
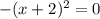
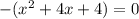
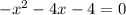
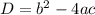
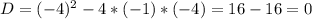
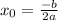
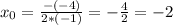
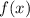взять полученное значение корня квадратного уравнения 
.
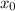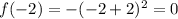
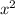стоит знак минус, то ветви параболы будут направлены вниз.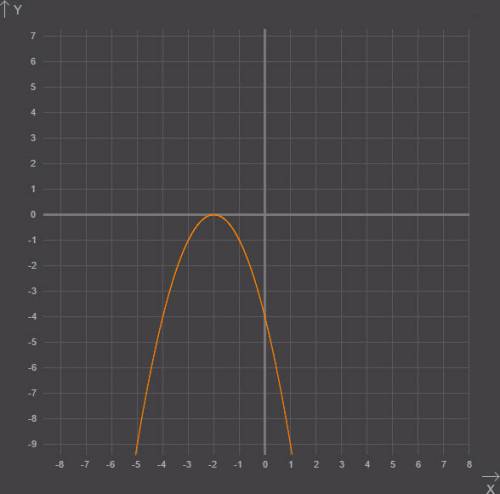
х = 2
Объяснение:
Ближайшая к 39 степень тройки, которая ее превышает, равна 81
Т.е. при x = 3 гарантированно решение
Теперь воспользуемся алгоритмом: от тройки будем идти все ниже и ниже до тех пор, пока неравенство не станет неверным. Последнее значение, которое обращало неравенство в верное - и будет наименьшим целым решением
При х = 2 имеем:
27 + 4*1 >= 39
39 >= 39
Значит при х = 2 неравенство тоже верно
Смотрим на х = 1
9 + 4 >= 39
13 >= 39
При х = 1 неравенство обращается в неверное. Значит х = 2 - минимально возможное значение в целых числах