Вот тут только первое задание:

У такой функции область значений ограничена только тем, что знаменатель не может быть равен нулю. Для нахождения этого условия решим квадратное уравнение:
3х^2 + 2x -1 = 0
D = 4 + 4*3 = 16 = 4^2
x1,2 = ( -2 +- 4 ) / 6 = {-1; 1/3}
То есть в точках х=-1 и х=1/3 функция имеет разрывы.
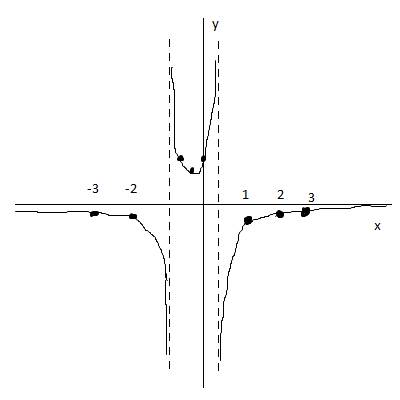
Далее график в принципе можно построить по точкам с учётом, что это будет гипербола (так как х присутствует только в знаменателе) и скорее всего он будет уходить в бесконечность и менять знак в точках разрывов.
Возьмём точки например:
х=1 тогда y=-1/(3+2-1)=-1/4
x=2 тогда y=-1/(12+4-1)=-1/15
x=3 y=-1/(27+6-1)=-1/32
Значит в правой части - гипербола от минус бесконечности растёт до нуля, и проходит через эти точки
х=-2 у=-1/(12-4-1)=-1/7
х=-3 y=-1/(27-6-1)=-1/20
Значит в левой части гипербола от нуля падает до минус бесконечности
Осталась центральная часть, тут она будет сначала падать от бесконечности и потом возрастать обратно. Наименьшего значения она достигнет посередине интервала. Найдём это точку:
х=-1/3 у=-1/(1/3-2/3-1)=3/4 - это минимум функции на интервале
И на всякий случай найдём пару вс точек:
х=0 тогда y=1
х=-2/3 y=-1/(4/3-4/3-1)=1
Через эти точки пройдёт график
На всякий случай прилагаю ужасающую иллюстрацию из пэинта, если что - спрашивайте
Ну что ж, возьмем числа в промежутке от нуля до ста, чтобы было легче
Конечно, лучше, чем считать до миллиона))
Числа, которые не делятся ни на 5, ни на 11 в этом промежутке - 71, так как на 5 делятся 20 чискл из 100, а на 11 делятся 9 чисел. В сумме 29. Из 100 вычитаем 29, получается 71.
Числа, которые делятся или на 2, или на 7 в этом промежутке - 51. Так как на 2 делятся 45 чисел, а на 7 - 6. В сумме 51. Может где-то и есть просчеты. НО зато видно, что чисел, которые не делятся на 5, или на 11 больше
жмем после того как появится второе решение). Выбирай мое))
На координатной плоскости нужно отметить эти точки, затем провести из этих точек прямые и отметить получившуюся точку !вот и все!