Определить промежутки монотонности функции, не используя производную функции.
y = (x² - x - 20)² - 18
=================================
Область определения функции D (y) = R
y = (x² - x - 20)² - 18
Квадратичная функция в квадратичной функции
y = f(z); z = g(x)
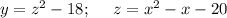
Чтобы найти промежутки монотонности квадратичной функции, нужно найти абсциссу вершины параболы.
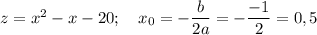- координата вершины
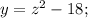z = 0 - координата вершины параболы
x₁ = -4; x₂ = 5 - координаты вершин параболы
Таким образом, есть три точки, которые определяют промежутки монотонности функции y = (x² - x - 20)² - 18.
x₁ = -4; x₀ = 0,5; x₂ = 5
x ∈ (-∞; -4] - функция убывает : y(-5) > y(-4)
x ∈ [-4; 0,5] - функция возрастает : y(-4) < y(0)
x ∈ [0,5; 5] - функция убывает : y(1) > y(2)
x ∈ [5; +∞) - функция возрастает : y(5) < y(6)
1.a=P:2-b 2.Площадь прямоугольного тр-ка = ав/2, где а и в его катеты. Пусть катет а=х. тогда катет в=х + 31. Площадь = х (х+31)/2=180 или х2 + 31х = 360 или х2 + 31х -360 =0 Решаем кв. ур-ие и находим х1 и х2. По ф-ле х1 = -40, х2 = 9. Значит катет а=9 (см), а катет в=9 + 31= 40 (см) 3.2х+7х=180; 9х=180; х=20. Коэффициент пропорциональности 20. Значит меньший угол, который 2х, равен 20*2=40 градусов. Больший угол 7х=140. ответ: 40 градусов.
4.1,7*0,01*1000=17кг
