Пусть, для определённости, d>=c>=b>=a. Тогда всю дробь можно переписать в виде:
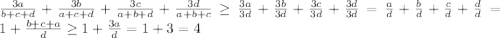
Что и требовалось доказать.
Пояснение: Выражение после первого знака неравенства получается, если взять наименьший знаменатель, а это d+d+d=3d.
Выражение после второго знака неравенства получается оттого, что мы берём наибольший числитель(то есть b+c+a=a+a+a=3a).
Выражение после третьего знака неравенства справедливо так как a>=d, то есть a/d>=1. Отсюда 3*(a/d)>=1*3=3
P.S. Если что-то непонятно, то не стесняйся спрашивать)
Для того, чтобы найти точку пересечения прямых, заданных уравнениями y = x + 2 и y = 3x - 2 мы с вами составим и решим систему линейных уравнений.
Система уравнений:
y = x + 2;
y = 3x - 2.
Решать систему уравнений будем одним из методов — методом подстановки. Давайте в первое уравнение системы вместо y подставим выражение из второго уравнений.
Система уравнений:
3x - 2 = x + 2;
y = x + 2;
3x - x = 2 + 2;
2x = 4;
x = 4 : 2;
x = 2.
Система уравнений:
x = 2;
y = x + 2 = 2 + 2 = 4.
ответ: (2; 4).
Объяснение:
1. (x⁴-x²-12)/(x³+1)=0
x⁴-x²-12=0 или x³+1≠0
x⁴-x²-12=0 биквадратное уравнение, x²=t, t>0
t²-t-12=0. t₁=4, t₂=-3. -3<0. t=-3 посторонний корень, => t=4
обратная замена: t=4. x²=4. x₁=-2, x₂=2
x³+1≠0, x³≠-1. x≠-1
(x-2)*(x+2)*(x²+3)/(x³+1)>0
- + - +
2. (-2)(-1)(2)>x
x∈(-2;-1)∪(2;∞)