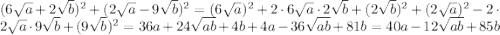5040
Объяснение:
Чтобы решить эту задачу, нужно использовать теорию вероятности.
У нас есть 7 разрядов, куда будут подставляться цифры (число 5720198 - семиразрядное) и 7 вариантов цифр для каждого разряда (5,7,2,0,1,9,8). Кроме того мы знаем, что цифры будут перестанавливаться, а значит каждый из вариантов цифр может появляться в примере только один раз. Все готово для решения.
В первом разряде может присутствовать любой из семи вариантов:
7
Во втором - на один меньше, так как один из вариантов уже присутствует в перовом разряде.
7*6
В третьем - еще на один меньше по той же причине
7*6*5
В итоге получаем следующий пример:
7*6*5*4*3*2*1 = 5040
В краткой форме это будет выглядеть так:
7!=5040
ответ: 5040 вариантов
В каждом из 8 разрядов могут располагаться четные числа 0,2,4,6,8 и нечетные числа 1,3,5,7,9.
Посчитаем, столько четных и нечетных сумм можно получить. Для этого запишем количество четных и нечетных чисел в каждом разряде в виде 5i+5j, где i - четные числа, а j нечетные числа.
При последовательном сложении всех возможных чисел в двух разрядах получим:
(5i+5j)(5i+5j)=5^2i+5^2ij+5^2ij+5^2j
Четное число при сложении с нечетным образует четное число, в остальных случаях образуется четное число, следовательно:
5^2i+5^2j=2*5^2i
5^2ij+5^2ij=2*5^2j
То есть при сложении чисел из двух разрядов (от 00 до 99)образуется 50 четных и 50 нечетных чисел. То есть количество четных/нечетных чисел, полученных в результате суммы, тождественно количеству четных/нечетных чисел от 0 до 99. Прибавляя числа из других разрядов, легко заметить, что это тождество сохраняется. Таким образом, задача сводится к вычислению количества нечетных чисел на участке от 10000000 до 99999999.
50000000-9999999=40000001
1)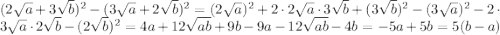
2)