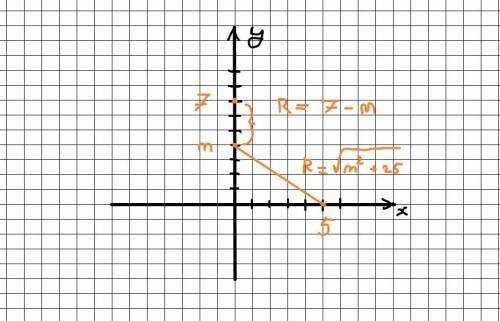
Пусть точка C(0, m) - центр окружности (так как по условию центр лежит на оси OY, то первая координата равна 0)
Известно, что расстояние от центра до любой точки на окружности является константой и равно радиусу R окружности
Наша окружность проходит через точку 7 на оси OY, значит R = 7 - m
Также окружность проходит через точку 5 на оси OX, значит по теореме Пифагора 
Приравняем это и получим уравнение:
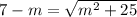
Возвёдём в квадрат и решим уравнение:

Координата центра окружности - 
Радиус окружности: 
Уравнение окружности выглядит следующим:

Подставим наши числа:
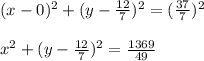
ответ: 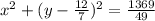
4x-10y=45; 4x-10y=45;
8x= 79, x=9.875, 4*9.875 +10y=34, 39.5+10y=34,
10y= 34-39.5 , 10y=-5.5, y=-0.55
ответ: уравнение имеет единственное решение (9.875;-0.55)