ответ:
y' = 4x^3-4x
приравниваем ее к нулю:
4x^3-4x = 0
x1 = 0
x2 = -1
x3 = 1
вычисляем значения функции
f(0) = 8
f(-1) = 7
f(1) = 7
fmin = 7, fmax = 8
используем достаточное условие экстремума функции одной переменной. найдем вторую производную:
y'' = 12x^2-4
вычисляем:
y''(0) = -4< 0 - значит точка x = 0 точка максимума функции.
y''(-1) = 8> 0 - значит точка x = -1 точка минимума функции.
y''(1) = 8> 0 - значит точка x = 1 точка минимума функции.
объяснение:
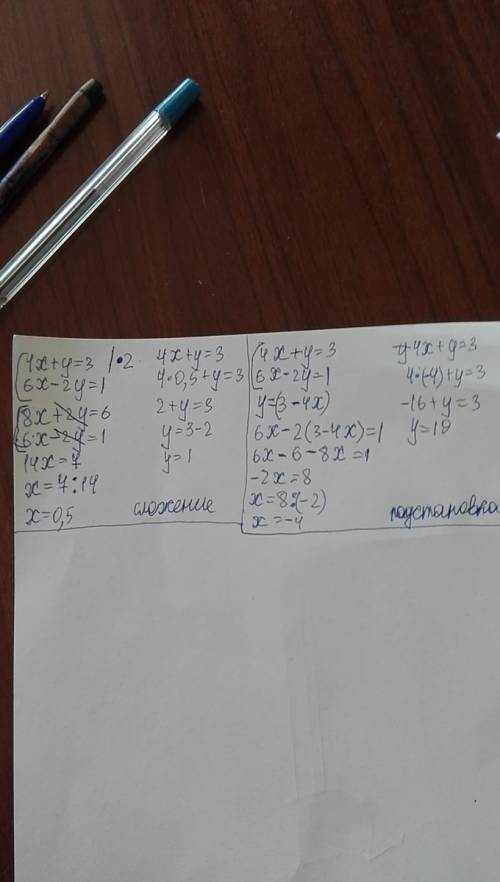
4х+у=3 |×2
6х-2у=1
8x+2y=6
6x-2y=1
8x+2y +6х-2у=6+1
14х= 7
х=7/14=1/2
х= 0,5
у= 3-4х
у= 3- 4*0,5 = 3-2=1
ответ: (0,5 ;1)
Метод подстановки.
у=3-4х
6х-2у=1
6х -2(3-4х) =1
6х-6+8х=1
14х=1+6
х=7/14
х=0,5
у= 3-4*0,5=3-2=1
ответ: (0,5 ; 1) .