Найдите острый угл параллелограмма стороны которого равны 14м и 8м , а площадь 56м в квадрате

👇

Увидеть ответ

Ответ:

Polinkamalina2017

06.04.2021

S=a*b*sinα
sinα=s/ab=56/112=0.5
α=30°

4,4(16 оценок)

Открыть все ответы

Ответ:

Almazik20056

06.04.2021

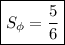3) $\boxed{S_{\phi} = \dfrac{5}{6}}$ квадратных единиц

4) 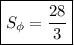$\boxed{S_{\phi} = \dfrac{28}{3}}$ квадратных единиц

Объяснение:

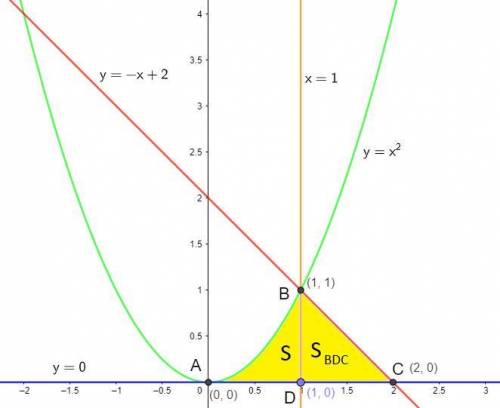
По условию фигура ограничена линиями:

$y = x^{2}$

y = 0

y = -x + 2

Линии ограничивают область (закрашенную желтым цветом и которую можно назвать ABC).

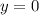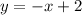Прямые y = 0 и y = -x +2 имеют пересечения в точке C(2;0).

0 = -x + 2 ⇒ x = 2; y(-2) = 0

Прямые 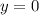y = 0 и $y = x^{2}$ имеют пересечения в точке A(0;0).

Прямые 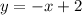y = -x + 2 и $y = x^{2}$ имеют пересечения в точке B(0;0).

$-x + 2 = x^{2}$

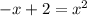
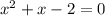
$x^{2} + x - 2 = 0$

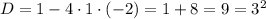
$D = 1 - 4 \cdot 1\cdot (-2) =1 + 8 = 9 = 3^{2}$

$x_{1} = \dfrac{-1 + 3}{2} = \dfrac{2}{2} = 1$

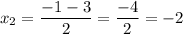
$x_{2} = \dfrac{-1 -3}{2} = \dfrac{-4}{2} = -2$

Однако так как нас согласно расположению графиков относительно друг друг друга, то нас интересует 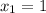$x_{1} = 1$ , то есть точка B(1;1).

Проведем прямую x = 1. Таким образом она разбила желтую часть на две фигуры. Где площадь криволинейно трапеции ABD с пределами интегрирования от 0 до 1 можно найти с определенного интеграла, а оставшуюся площадь, как площадь треугольника BDC. То есть площадь фигуры имеет вид: 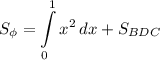$S_{\phi} = \displaystyle \int\limits^1_0 {x^{2} } \, dx + S_{BDC}$ .

а) 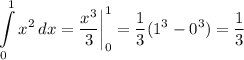$\displaystyle \int\limits^1_0 {x^{2} } \, dx = \dfrac{x^{3}}{3} \bigg | _0^1 = \dfrac{1}{3}(1^{3} - 0^{3}) = \dfrac{1}{3}$ квадратных единиц.

б) 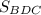$S_{BDC}$

Так как отрезок BD треугольника ΔBDC лежит на прямой x = 1, то треугольник ΔBCD - прямоугольный с катетами BD и DC.

Зная координаты точек B(1;1),D(1;0),C(2;0) найдем длинны отрезков BD и DC. 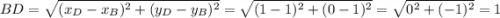$BD = \sqrt{(x_{D} - x_{B})^{2} + (y_{D} - y_{B})^{2}} = \sqrt{(1 - 1)^{2} + (0 - 1)^{2}} = \sqrt{0^{2} + (-1)^{2}} = 1$ .

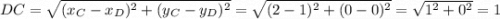$DC = \sqrt{(x_{C} - x_{D})^{2} + (y_{C} - y_{D})^{2}} = \sqrt{(2 - 1)^{2} + (0 - 0)^{2}} = \sqrt{1^{2} + 0^{2}} = 1$ .

По формуле площади прямоугольного треугольника (ΔBDC) :

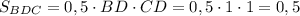$S_{BDC} = 0,5 \cdot BD \cdot CD = 0,5 \cdot 1 \cdot 1 = 0,5$ квадратных единиц.

в) Площадь фигуры: 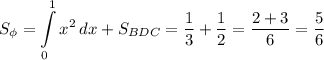$S_{\phi} = \displaystyle \int\limits^1_0 {x^{2} } \, dx + S_{BDC} = \dfrac{1}{3} + \dfrac{1}{2} = \dfrac{2 + 3}{6} = \dfrac{5}{6}$ квадратных единиц.

По условию фигура ограничена линиями:

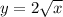
$y = 2\sqrt{x}$

y = 0

x = 1

x = 4

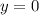
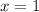
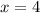
Пределы интегрирования:

a = 1

b = 4

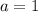
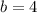
Найдем площадь криволинейной трапеции по определению:

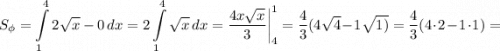
$S_{\phi} = \displaystyle \int\limits^4_1 {2\sqrt{x} - 0 } \, dx = \displaystyle 2 \int\limits^4_1 {\sqrt{x} } \, dx = \dfrac{4x\sqrt{x} }{3} \bigg | _4^1 = \dfrac{4}{3} (4\sqrt{4} - 1\sqrt{1)} = \dfrac{4}{3}(4 \cdot 2 - 1 \cdot 1)=$

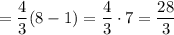$= \dfrac{4}{3}(8 - 1) = \dfrac{4}{3} \cdot 7 = \dfrac{28}{3}$ квадратных единиц.

4,6(87 оценок)

Ответ:

freedomman87

06.04.2021

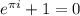
$e^{\pi i}+1=0$

Это тождество Эйлера, являющееся частным случаем формулы Эйлера 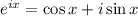$e^{ix} = \cos x + i\sin x$ при $x = \pi$ .

Тождество объединяет между собой пять фундаментальных чисел из разных областей математики, связь между которыми на первый взгляд неочевидна:

1) основание натурального логарифма (алгебра);

2) отношение длины окружности к ее диаметру 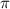$\pi$ (геометрия);

3) мнимую единицу (комплексные числа);

4) нейтральный элемент относительно умножения 1 (арифметика);

5) нейтральный элемент относительно сложения 0 (арифметика).

Тождество примечательно в первую очередь своей простотой и элегантностью. Так, Ричард Фейнманн называл его "самой замечательной формулой в математике".

Примечательна фраза профессора Гарвардского университета Бенджамин Пирса, произнесенная после доказательства тождества Эйлера: "мы не можем понять её [формулу], и мы не знаем, что она значит, но мы доказали её, и поэтому мы знаем, что она должна быть достоверной".

4,8(58 оценок)

Это интересно:

Компьютеры-и-электроника

07.02.2023

Как записать DVD диск: подробное руководство...

Кулинария-и-гостеприимство

23.03.2020

Простой и вкусный рецепт вегетарианской лазаньи, который вы полюбите...

Хобби-и-рукоделие

17.12.2021

Как починить молнию, если бегунок полностью соскочил...

Дом-и-сад