На расстоянии метра одно от другого лежат в ряд сто яблок, и в том же ряду на расстоянии метра слева от первого яблока садовник принес и поставил корзину. спрашивается, какой длины путь он совершит, если возьмется собирать
эти яблоки так, чтобы брать их последовательно одно за другим и каждое отдельно относить в корзину, которая все это время стоит на одном и том же месте?
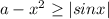
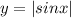 расположен выше оси ОХ.
расположен выше оси ОХ. 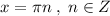 .
.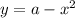 - это параболы , ветви
- это параболы , ветви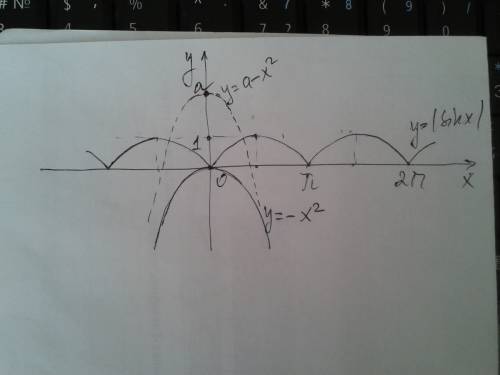
Расстояние до каждого яблока садовник будет проходить дважды. Для удобства счета 100 слагаемых следует разбить на 50 пар:
S=(1+2+3+...+99+100)*2=((1+100)+(2+99)+(3+98)+...+(50+51))*50)*2=101*100=10100 (м)
10100 м=10,1 км
ответ: путь длиной 10,1 км.