Алгебра: Решите комплексные числа вычислите: 4i/1+i

Решите комплексные числа вычислите: 4i/1+i

👇

Увидеть ответ

Ответ:

Kosty12541

07.01.2023

4i/(1+i)=4i*(1-i)/[(1+i)(1-i)]=4i(1-i)/(1+1)=2i*(1-i)=2i+2

4,7(32 оценок)

Открыть все ответы

Ответ:

Selebruty1

07.01.2023

Задание №1

а). 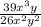$\frac{39x^{3}y }{26x^{2} y^{2} }$ (сокращаем на "13 $x^{2}$ y")

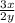
$\frac{3x}{2y}$

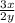
ответ: $\frac{3x}{2y}$

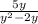б). $\frac{5y}{y^{2}-2y }$ (в знаменателе выносим "y" и сокращаем с "y" в числителе)

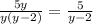
$\frac{5y}{y(y-2)} = \frac{5}{y-2}$

ответ: 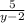$\frac{5}{y-2}$

в). 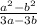$\frac{a^{2}-b^{2} }{3a-3b}$ (раскрываем числитель по формуле разности квадратов 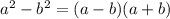$a^{2} -b^{2} = (a-b)(a+b)$ , в знаменателе выносим "3")

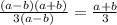
$\frac{(a-b)(a+b)}{3(a-b)} = \frac{a+b}{3}$

ответ: 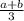$\frac{a+b}{3}$

Задание №2

а). 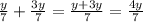$\frac{y}{7}+\frac{3y}{7} = \frac{y+3y}{7} = \frac{4y}{7}$ (одинаковый знаменатель, значит можно складывать)

ответ: 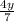$\frac{4y}{7}$

б). 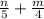$\frac{n}{5}+\frac{m}{4}$ (знаменатели разные, чтобы сложить приводим к общему знаменателю. Первую дробь умножаем на 4, вторую умножаем на 5, после чего складываем)

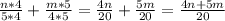
$\frac{n*4}{5*4}+\frac{m*5}{4*5}= \frac{4n}{20} +\frac{5m}{20} = \frac{4n+5m}{20}$

ответ: 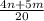$\frac{4n+5m}{20}$

в). $\frac{3}{2a}-\frac{5}{3a}$ (принцип тот же. "а" есть и там, и там в знаменателе, значит первую дробь умножаем на 3, вторую умножаем на 2, чтобы получить общий знаменатель, после чего вычитаем)

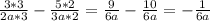
$\frac{3*3}{2a*3}-\frac{5*2}{3a*2} = \frac{9}{6a}-\frac{10}{6a} = -\frac{1}{6a}$

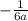
ответ: $-\frac{1}{6a}$

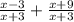г). $\frac{x-3}{x+3}+\frac{x+9}{x+3}$ (знаменатель одинаковый - складываем)

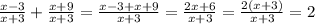
$\frac{x-3}{x+3}+\frac{x+9}{x+3} = \frac{x-3+x+9}{x+3}= \frac{2x+6}{x+3}=\frac{2(x+3)}{x+3} = 2$

ответ: 2

Задание №3

а). 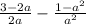$\frac{3-2a}{2a} -\frac{1-a^{2} }{a^{2} }$ (умножаем первую дробь на a, а вторую умножаем на 2, после чего вычитаем дроби)

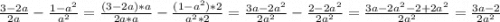
$\frac{3-2a}{2a} -\frac{1-a^{2} }{a^{2} } = \frac{(3-2a)*a}{2a*a}-\frac{(1-a^{2})*2}{a^{2}*2} = \frac{3a-2a^{2} }{2a^{2} } -\frac{2-2a^{2} }{2a^{2} } = \frac{3a-2a^{2}-2+2a^{2} }{2a^{2} } = \frac{3a-2}{2a^{2} }$

ответ: 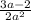$\frac{3a-2}{2a^{2} }$

б). $\frac{1}{3x+y}-\frac{1}{3x-y}$ (первую дробь умножаем на знаменатель второй дроби, а вторую дробь умножаем на знаменатель первой дроби, после чего вычитаем)

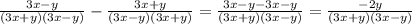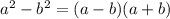$\frac{3x-y}{(3x+y)(3x-y)} -\frac{3x+y}{(3x-y)(3x+y)} = \frac{3x-y-3x-y}{(3x+y)(3x-y)}= \frac{-2y}{(3x+y)(3x-y)}$ (ещё можно свернуть по формуле разности квадратов $a^{2} -b^{2} = (a-b)(a+b)$ )

ответ: 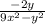$\frac{-2y}{9x^{2}-y^{2} }$

в). $\frac{3}{b-2}-\frac{4-3b}{b^{2}-2b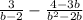}$ (вынесем "b" в знаменателе второй дроби за скобку и умножим первую дробь на "b", после чего вычитаем)

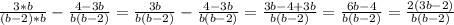
$\frac{3*b}{(b-2)*b}-\frac{4-3b}{b(b-2)} = \frac{3b}{b(b-2)} -\frac{4-3b}{b(b-2)} = \frac{3b-4+3b}{b(b-2)} = \frac{6b-4}{b(b-2)} = \frac{2(3b-2)}{b(b-2)}$

ответ: 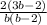$\frac{2(3b-2)}{b(b-2)}$

Задание №4

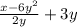$\frac{x-6y^{2} }{2y} +3y$ (приведем к общему знаменателю умножив 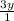$\frac{3y}{1}$ на "2y", после чего сложим)

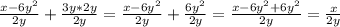$\frac{x-6y^{2} }{2y} +\frac{3y*2y}{2y} = \frac{x-6y^{2} }{2y} + \frac{6y^{2} }{2y} = \frac{x-6y^{2}+6y^{2} }{2y} = \frac{x}{2y}$ (теперь подставляем x = -8 и y = 0,1. Десятичное число 0,2 = дроби 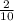$\frac{2}{10}$ . Когда получилась трёхэтажная дробь, то знаменатель дроби в знаменателе переносится в числитель и умножается на числитель общей дроби, а знаменатель становится числитель дроби в знаменателе)

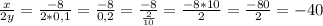
$\frac{x}{2y} = \frac{-8}{2*0,1}= \frac{-8}{0,2}= \frac{-8}{\frac{2}{10} } = \frac{-8*10}{2} = \frac{-80}{2} = -40$

ответ: -40

Задание №5

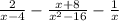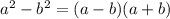$\frac{2}{x-4}-\frac{x+8}{x^{2}-16} -\frac{1}{x}$ (знаменатель средней дроби раскроем по формуле разности квадратов $a^{2} -b^{2} = (a-b)(a+b)$ .

Первую дробь умножим на "х" и на "x+4", среднюю дробь умножим на "х", а третью дробь умножим на "x+4" и на "x-4", после чего посчитаем)

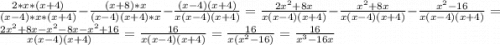$\frac{2*x*(x+4)}{(x-4)*x*(x+4)}-\frac{(x+8)*x}{(x-4)(x+4)*x} -\frac{(x-4)(x+4)}{x(x-4)(x+4)} = \frac{2x^{2}+8x}{x(x-4)(x+4)}-\frac{x^{2}+8x}{x(x-4)(x+4)}-\frac{x^{2}-16}{x(x-4)(x+4)} =\frac{2x^{2}+8x-x^{2}-8x-x^{2}+16}{x(x-4)(x+4)} =\frac{16}{x(x-4)(x+4)} = \frac{16}{x(x^{2}-16)} = \frac{16}{x^{3}-16x}$ ответ: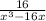 $\frac{16}{x^{3}-16x}$

4,6(28 оценок)

Ответ:

Матюха2005

07.01.2023

Случайное событие определено как событие, которое при осуществлении совокупности условий эксперимента может произойти или не произойти. Если при вычислении вероятности события никаких других ограничений, кроме условий эксперимента, не налагается, то такую вероятность называют безусловной; если же налагаются и другие дополнительные условия, то вероятность события называют условной. Например, часто вычисляют вероятность события B при дополнительном условии, что произошло событие А.

Условной вероятностью PA(B)=P(B|A) (два обозначения) называют вероятность события В, вычисленную в предположении, что событие А уже наступило.

Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность второго, вычисленную при условии, что первое событие произошло, т.е.

P(AB)=P(B)⋅P(A|B)=P(A)⋅P(B|A).

В частности, отсюда получаем формулы для условной вероятности:

P(A|B)=P(AB)P(B),P(B|A)=P(AB)P(A).

4,8(85 оценок)

Это интересно:

Стиль-и-уход-за-собой

31.01.2023

Как избавиться от раздражения кожи после бритья: полезные советы и трюки...

Стиль-и-уход-за-собой

05.08.2021

Как правильно надеть кимоно: советы и рекомендации...

Взаимоотношения