Объяснение:
4 < b < 7 (1)
подобные примеры решаются просто - домножаем все части неравенства, прибавляем/отнимаем от всех частей нужные числа, пока не получим посередине, то, что требуется в доказательстве
1) надо в средней части получить 13- 3b
умножим все части (1) на -3 (здесь помним, при умножении на отрицательное число знаки неравенства меняются на противоположные)
-12 > -3b > -21 (2)
добавим ко всем частям (2) +13
-12 + 13 > 13-3b > -21 +13 или -8 < 13-3b < 1 -что и требовалось доказать
2) здесь пойдем от обратного
если 1/m < 1/n, то это значит, что m < n
и тогда из нашего ответа
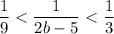
перепишем неравенство для знаменателей
получим
3 < 2b-5 < 9
теперь нам надо получить в середине b
прибавляем ко всем частям +5 и потом делим все части на 2
3+5 < 2b < 9+5
8 < 2b < 14
4 < b < 7 это и есть наша формула (1)
неравенство доказано.
1. |x²-7|+12=0
|x²-7|=-12
x∈∅
Данное уравнение не имеет корней, т.к. модуль является неотрицательным числом.
2. Выделим полный квадрат:
x²-6x+8 = (x²-2x*3+3²) -3²+ 8 = (x-3)² -9 + 8 = (x-3)² -1
Разложим на множители x²-6x+8 = (x-x₁)(x-x₂)
По теореме Виета находим корни: х₁*х₂=8 и х₁+х₂=-6 => х₁=2 и х₂=4
x²-6x+8= (x-2)(x-4)
3. 3x²-6x+c=0, x₁=x₂
По условию, квадратное уравнение имеет равные корни, следовательно, дискриминант этого уравнения равен нулю.
Находим с:
D= (-6)²-4*3*c = 36-12c
36-12c = 0
12c = 36
c = 3
х<у