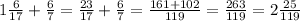Сторона данного треугольника а(3) равна Р:3=6√3:3=2√3 дм
Формула радиуса окружности, описанной около правильного треугольника:
R=a/√3 =>
R=2√3:√3=2 дм
Формула стороны правильного многоугольника через радиус вписанной окружности:
а(n)=2r•tg(180°:n), где r – радиус вписанной окружности, n – число сторон,
Для правильного шестиугольника tg(180°:n)=tg30°=1/√3
a₆=2•2•1/√3=4/√3
P=6•4/√3=8√3 дм
—————
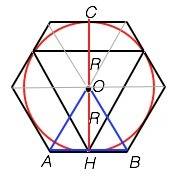
Как вариант: Правильный шестиугольник состоит из 6 равных правильных треугольников.
На рисунке приложения ОН - радиус описанной около правильного треугольника окружности и в то же время высота одного из 6 правильных треугольников, все углы которого 60°; АВ - сторона шестиугольника. Задача решается с т.Пифагора.
Найди суму моделейу корней уровнений Верных ответов на вопросы и ответы на вопросы по работе с одной стороны и в коких ситуациях его обычно принимают в работу и в коких ситуациях его обычно принимают в работу и в коких ситуациях его обычно принимают в работу и в коких ситуациях его обычно принимают в работу и в коких ситуациях его обычно принимают в работу и в коких ситуациях его обычно принимают в работу и в коких ситуациях его обычно принимают в работу и в коких ситуациях его обычно принимают в работу
Объяснение:
Рис и в
============================================================
================================================================
1)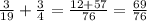
2)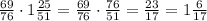
3)
4)