пусть первое число равно х, а второе у. Тогда 2х+у=11, а x^2+y^2=25.
Получаем систему уравнений:
2х+у=11;
x^2+y^2=25.
Выразим из первого уравнения у:
у=11-2х
и подставим полученное значение во втрое:
x^2+(11-2x)^2=25
x^2+121-44x+4x^2=25
5x^2-44x+121-25=0
5x^2-44x+96=0
Найдем дискриминант квадратного уравнения
D=b^2-4ac=1936-4*5*96=16
Так как дискриминант больше нуля то, квадратное уравнение имеет два корня:
x1=(-b+√D)/(2a)=(44+√16)/(2*5)=4.8
x2=(-b-√D)/2a=(44-√16)/(2*5)=4
В условии задачи сказано, что взяты натуральные числа, значит, нам подходит только х=4
Найдем у:
у=11-2х
у=11-2*4
у=3
ответ: взяты числа 4 и 3
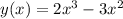
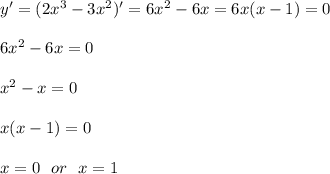
![+++++++[0]---------[1]+++++++\ \textgreater \ x](/tpl/images/0904/9591/fbfbf.png)
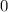являеться максимумом функции 
,
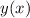являеться минимумом функции 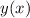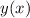монотонно растет на промежутке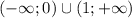 
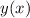монотонно убывает на промежутке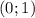 
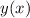пересекает ось ОХ в точкаx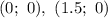 
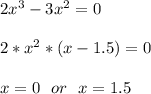
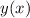пересекает ось ОУ в точке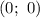 
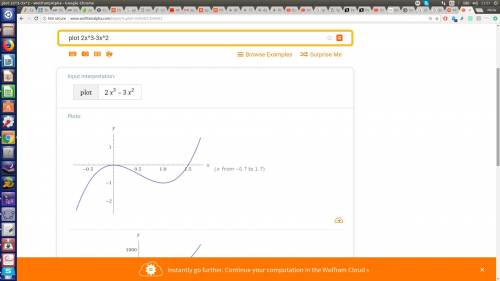
Y= x - 2
решить систему уравнений
Y=x² – 4x + 4
Y= x - 2 ⇔ x² – 4x + 4 =x-2 x² – 5x + 6=0
x1=3 x2=2
Y= x - 2 y1=3-2=1 y2=2-2=0
проверка
1) x1=3
y1=1
1=3² – 4·3 + 4 1=1 верно
1= 3 - 2 верно
2) x2=2
y2=00=2² – 4·2 + 4 верно
0= 2 - 2 верно
ответ: x1=3 y1=1 ; x2=2 y2=0.