Биномиальное распределение стремится к нормальному при больших n
По условию
р = 0.9
соответственно
q = 1- p = 0.1
Математическое ожидание
М= np= 1000 * 0.9 = 900
Дисперсия
D= npq = 1000*0.9*0.1= 90
Сигма = √D= 3√10 = ~9.5
Мы рассматриваем интервал от центра распределения 900 до 940 - это больше чем четыре сигмы.
В этом случае в табличку нормального распределения можно даже не заглядывать, хвостик за четыремя сигмами очень малюсенький, пятый знак после запятой.
Половина всей выборки до 900 , половина после.
ответ
Вероятность равна ~0.5
y=11+6√x-2x√x D(f)=x∈(0:+∞)
2x√x=2*x¹*x¹/₂=2*x³/²
6√x=6*x¹/²
f(x)=-2*x³/²+6*x¹/²+11
(2*x³/²)`=3*x¹/²=3√x
(6*x¹/²)`=3/x¹/²=3/√x
(11)`=0
f`(x)=-3√x+3/√x
Приравниваем производную к нулю:
-3√x+3/√x=0
-3√x*√х+3=0
-3х+3=0
-3х=-3
х=1 - критическая точка.
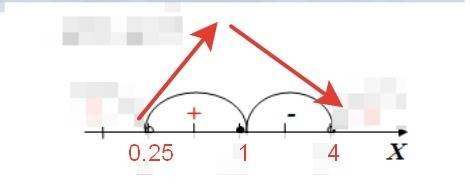
Чтобы узнать, достигает ли функция максимума в точке экстремума х=1, нужно определить знаки производной методом интервалов (рисунок во вложении):
f`(1)=0
f`(0.25)=-3√0.25+3/√0.25=4.5>0 - функция возрастает на отрезке (0;1)
f`(4)=-3√4+3/√4=-4.5<0 - функция убывает на отрезке (1;+∞)
При переходе через точку х=1 производная меняет знак с "+" на "-", значит х=1 - точка максимума функции.