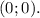
Объяснение:
Данная функция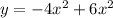 
является квадратичной функцией (многочлен второй степени) и задаёт квадратичную параболу. Как известно, у такой функции может быть лишь один экстремум, находящийся в вершине параболы.
Упростим исходную функцию: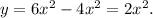 
Для нахождения 
единственного экстремума воспользуемся производной: 
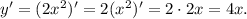
По лемме Ферма, значение производной от экстремума нулевое. Таким образом, точки экстремума будет решением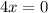 
.
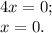
Для нахождения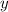 
точки экстремума вычислим значение исходной функции от найденного :
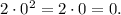
Получается, что координаты точки экстремума это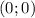 
.
ответ: 24 см и 12 см.
Объяснение:
Пусть l - длина отрезка, соединяющего середины диагоналей трапеции. Этот отрезок лежит на средней линии трапеции и равен полуразности её оснований. Пусть a и b - основания трапеции, причём a>b, а c - длина средней линии трапеции. Так как по условию диагонали трапеции делят её среднюю линию на 3 равных части, то l=c/3. Отсюда c=3*l=3*6=18 см и, так как c=(a+b)/2, то мы получаем систему уравнений:
(a-b)/2=6
(a+b)/2=18
или:
a-b=12
a+b=36
Решая её, находим a=24 см и b=12 см.
Sin 2a=2*sin a*cos a
Sin 3a=3*sin a*cos^2 a-sin^3 a=3*sin а*(1-2*sin^2 a).
Далее делишь и получаешь 3(1-2*sin^2 a)/2*cos a