
Объяснение:
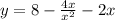
На 0 делить нельзя. Область определения: (-∞;0)∪(0;∞)
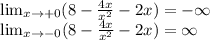
Т.к х не равен 0, то точек пересечения с осью у нет. Находим точки пересечения с осью х.
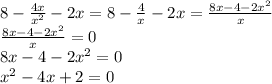
Решаем квадратное уравнение, находим точки пересечения с осью х:
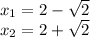
Находим точки экстремума (производная равна нулю).
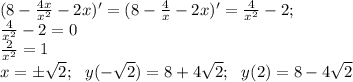
Для нахождения точек перегиба находим вторую производную
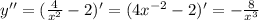
Вторая производная нигде не равна нулю, точек перегиба нет.
Горизонтальных асимптот нет. Вертикальная асимптота одна: х=0.
Ищем наклонную асимптоту:
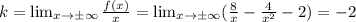
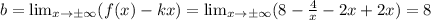
Наклонная асимптота есть:
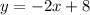
Дальнейшее исследование проводим, заполняя таблицу (см. рис.1).
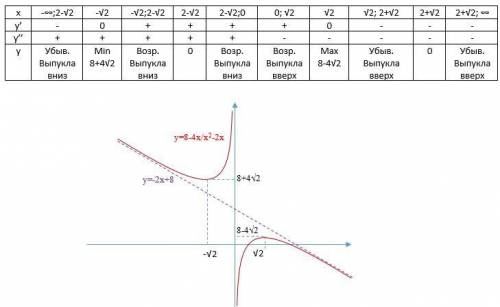
- + - +
____₀______₀_____₀____
- 2 2 6
///////// ////////////
ответ : x ∈ (- ∞ ; - 2) ∪ (2 ; 6)
+ - + - +
____₀_____₀____₀____₀____
- √15 - 3 0 √15
//////////// ///////////
ответ : x ∈ (- √15 ; - 3) ∪ ( 0 ; √15)
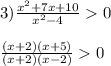
+ - - +
____₀_____₀_____₀____
- 5 - 2 2
///////// //////////
ответ : x ∈ (- ∞ ; - 5) ∪ (2 ; + ∞)
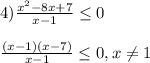
- - +
______(1)_____[7]_____
/////////// ////////////
ответ : x ∈ (- ∞ ; 1) ∪ (1 ; 7)
2)нули функции:
2x²+7x-4=0
D=49-4*2*(-4)=49+32=81
x1=(-7+9):4=2/4=1/2=0,5
x2=(-7-9):4=-16/4=-4
ответ:(-4;0,5)