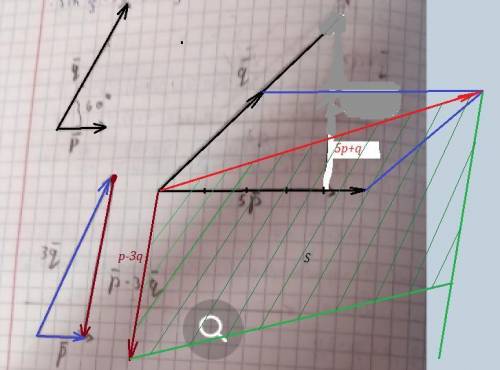
Вектор 5р : рисуем того же направления, что и вектор р, только в 5 раз длиннее.
Вектор q рисуем с параллельного переноса, совместив его начало с началом вектора 5р . Угол в 60 градусов сохраняется.
По правилу параллелограмма - диагональ параллелограмма, построенного на векторах 5р и q , является суммой этих векторов. Диагональ выходит из точки, являющейся общим началом векторов 5р и q .
Далее строим вектор 3q , длина которого в 3 раза больше длины вектора q , а направление совпадает с направлением вектора q .
Вектор ( р-3q ) - это сторона треугольника, соединяющая конец вектора 3q и начало вектора р . Причём векторы р и 3q имеют общее начало . Направление вектора (р-3q) идёт от вектора 3q к вектору р . На рисунке этот параллелограмм заштрихован зелёной штриховкой .
Чтобы построить параллелограмм, площадь которого равна векторному произведению векторов (5p+q) и (р-3q) , надо опять выбрать точку, которая будет началом как вектора (5р+q) , так и вектора (р-3q) . Затем достроить параллелограмм .
![(5p+q)\times (p-3q)=5[\, p\times p\, ]-15[\, p\times q\, ]+[\, q\times p\, ]-3[\, q\times q\, ]=\\\\=5\cdot 0-15[\, p\times q\, ]-[\, p\times q\, ]-3\cdot 0=-16[\, p\times q\, ]\\\\S=\Big |\, -16\cdot [\, p\times q\, ]\, \Big |=16\cdot |\, p\, |\cdot |\, q\, |\cdot sin60^\circ =16\cdot |\, p\, |\cdot |\, q\, |\cdot \frac{\sqrt3}{2}=\\\\=8\sqrt3\cdot |\, p\, |\cdot |\, q\, |](/tpl/images/1012/8562/61754.png)