Объяснение:
нам для решения нужны два свойства. логарифм числа а по основанию а равен единице, логарифм числа а в степени к по любому основанию равен к умножить на логарифм числа а по любому основанию. Как мы знаем если домножить число на единицу, оно не изменится, тогда
домножим правую часть первого уравнения на логарифм числа 6 по основанию 6, а второе уравнение на логарифм числа 18 по основанию 18, тогда
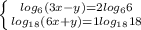 . уберем в 1-ом уравнении двойку в степень подлогарифмического, получим логарифм числа 36 по основанию 6. Теперь при равенстве логарифмов по одному основанию левых и правых частей, перейдем к равенству, подлогарифмических левых и правых частей, но теперь нужно учесть, что значения переменной х и у должны удовлетвореть ОДЗ: а именно, подлогарифмические выражение должны быть больше нуля, т.е. 3x-y>0 6x+y>0.
. уберем в 1-ом уравнении двойку в степень подлогарифмического, получим логарифм числа 36 по основанию 6. Теперь при равенстве логарифмов по одному основанию левых и правых частей, перейдем к равенству, подлогарифмических левых и правых частей, но теперь нужно учесть, что значения переменной х и у должны удовлетвореть ОДЗ: а именно, подлогарифмические выражение должны быть больше нуля, т.е. 3x-y>0 6x+y>0.
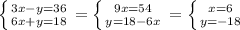 Проверим корни на принадлежность ОДХ
Проверим корни на принадлежность ОДХ
3*6-(-18) больше нуля.
6*6-18 так же больше нуля, значит эта пара чисел и есть решение системы.
2)
домножим 4 на логарифм 3 по основанию 3, и отправим 4 в степень, тогда
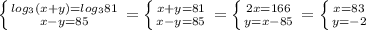 . Проверим ОДЗ
. Проверим ОДЗ
х+у должно быть болье нуля и это верно. значит пара чисел 83 минус 2 - решение
3) Тут нужно вспомнить еще одно свойство, что сумма логарифмов по одному основанию равна логарифму произведения по этому основанию, тогда
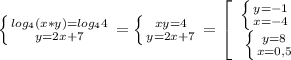 Т.к. по ОДЗ и икс и игрик должны быть больше нуля, то первая пара нас не устраивает, а значит ответ пара чисел 1/2 и 8
Т.к. по ОДЗ и икс и игрик должны быть больше нуля, то первая пара нас не устраивает, а значит ответ пара чисел 1/2 и 8
4)
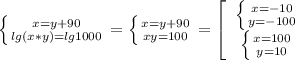 , икс и игрик должны быть положительны, поэтому только вторая пара 100 и 10 нас устраивает. (если что lg это десятичный логарифм, т.е. логарифм по основанию 10)
, икс и игрик должны быть положительны, поэтому только вторая пара 100 и 10 нас устраивает. (если что lg это десятичный логарифм, т.е. логарифм по основанию 10)
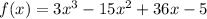
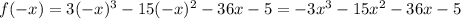
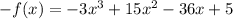
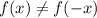 и
и 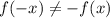 , то функция является функцией общего вида.
, то функция является функцией общего вида.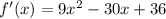
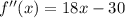
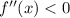
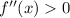
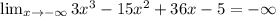
4a1+28d=20
a1+7d=5
a1=5-7d
S20=(2a1+19d)*20/10=(10-14d+19d)*10=(10+5d)*10=(d+2)*50