Вероятность посчитаем по классическому определению.
Общее число исходов равно числу сочетаний из 15 по 5, т.е. n=15!/(10!*5!)=(15*14*13*12*11)/(5*4*3*2*1)=7*3*13*11=3003,
число исходов, благоприятствующих наступлению события из 5 отличников выбрали 2 отличников, и из остальных (15-2) 13 студентов выбрали 3 не отличников, равно произведению числа сочетаний из
5 по 2, на число сочетаний из 13 по 3, т.е. m=(5!/(2!*3!))*(13!/(3!*10!))=10*286
(5!/(2!*3!))=(24*5)/12)=2*5=10; 13!/(3!*10!))=13*12*11/6=22*13=286
и искомая вероятность равна m/n=10*286/3003=2860/3003≈0.95
Вы решили неправильно!
Объяснение:
У Вас сам подход к решению неправильный. Складывается впечатление, что вы про формулы сокращенного умножения ничего не слышали.
Напомню, что:
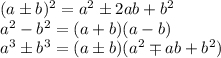
Это основные 5 формул.
Еще к этому нужно знать:
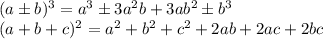
Понятно, что и для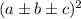 
нужно тоже знать формулы.
Это еще 5 формул.
И в заключение можно выучить формулы n-ой степени.
Теперь обратимся к решению вашего вопроса:
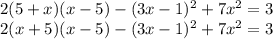
Что мы здесь видим? То, о чем я писал выше.
Перемножать надо? Нет! Пользуемся формулами:
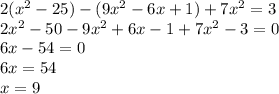
Уравнение решается в уме!
У Вас решение неправильное.
Уравнение решено!
tga=sina/cosa=15/17:(-8/17)=-15/17*17/8=-15/8
ctga=1/tga=-8/15