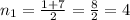
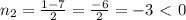, не подходит по условию, ведь n - натуральное число.
ответ: 22 литра.
Объяснение:
Пусть V л в минуту пропускает первая труба, тогда вторая в минуту пропускает V+1 л воды. Резервуар объёмом 462 л первая труба заполнит за время t1=462/V мин., а резервуар объёмом 374 л вторая труба заполнит за время t2=374/(V+1) мин. По условию, t1=t2+5 мин., откуда следует уравнение 462/V=374/(V+1)+5, которое приводится к квадратному уравнению 5*V²-83*V-462=0. Оно имеет решения V1=21 и V2=-4,4, но так как V>0, то V=V1=21 л. Тогда за 1 минуту вторая труба пропускает 21+1=22 л воды.
(x-1)* log(x+5)_(x+3) * log5_(x+5)^2 < 0;
(x -1)* log(x+5)_(x+3) * 2/ log(x+5)_5 < 0;
2 (x-1) * log(x+5)_(x+3) / log(x+5)_5 < 0;
Переходим к новому основанию 5
(x-1)* log5_(x+3) < 0;
Рассмотрим 2 случая
1) {x-1 >0; {x > 1; нет решений;
{log5_(x+3) < 0 {x+3< 1
2) {x- 1 < 0; {x< 1; - 2 < x < 1
log5_(x+3) > 0 x + 3 < 1;
пересекая с ОДЗ, получаем ответ
(-2; 1)