Пусть СЕ =х , тогда ВЕ= 32-х, АД= 16-х ВД= 24-(16-х) = 8+х. Треугольники ВДЕ и АВС подобны по двум углам ( угол в -общий , угол ВЕД= углу С как соответственные при параллельных ДЕ И АС и секущей ВС) Значит ВД/ ВА = ВЕ/ВС тоесть (8+х) : 24= (32-х) :4 , решаем эту пропорцию (8+х)* 32= (32-х)* 24
( 8+х)* 4= (32-х)* 3
32 +4х= 96 -3х
7х=64
х= 9 целых 1/7
ВД= 8+9 целых 1/7= 17 целых 1/7
Также пропорциональны стороны ВД : АВ= ДЕ : АС подстави данные 17 целых 1/7 : 24= ДЕ : 28, ДЕ = 17 целых 1/7 * 28 :24 = 20 см
ответ 20см
А (
; - 4)
Объяснение:
Если графики функций пересекаются, то у них есть общая точка. То есть есть какая-то точка А, которая принадлежит обоим графикам. Всё, что нам нужно сделать: найти её координату х и её координату у. Один из без выполнения графика:
1. приравниваем правые части и, прорешав уравнение, находим координату х:
-14х - 2 = 7х - 5
-14х - 7х = -5 + 2
- 21 х = -3 / : (- 21)
х =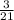 
(сокращаем дробь)
х =
2. подставляем найденное значение координаты х в любую из функций (куда удобнее) и находим координату у:
у = 7 · - 5 = 1 - 5 = -4
ответ: т. А (; - 4) - точка пересечения графиков функций у = - 14х - 2 и у = 7х - 5
