1.
а)
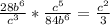
б)
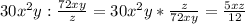
в)
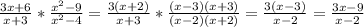
г)
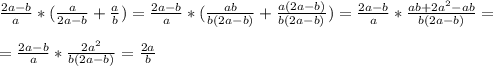
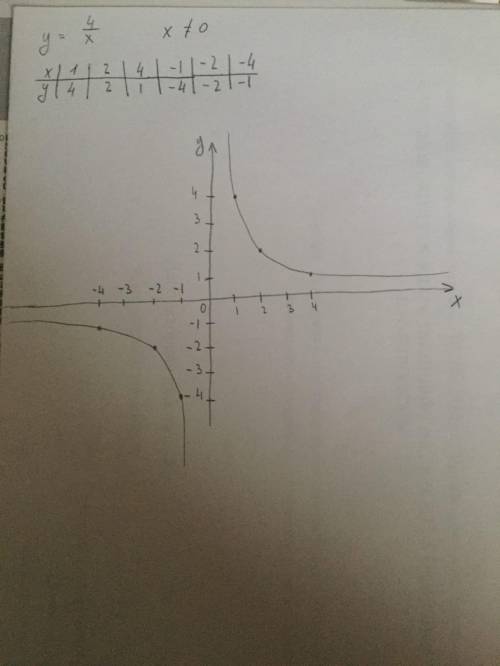
2. График на фото.
Область определения:
D(f)=(-∞;0)∪(0;+∞)
Функция принимает положительные значения при всех положительных Х, кроме 0(так как при нем знаменатель будет равен нулю).
3.
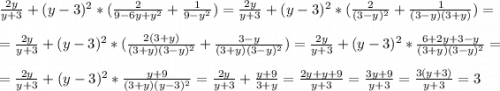
Получаем, что при всех значениях Y(кроме +-3) значение выражение будет равно 3, то есть какой бы Y мы не взяли, данное выражение всегда будет давать в ответе 3, что говорит о том, что оно не зависит от Y.
4.
Данное выражение имеет смысл при всех Х, кроме тех, при которых знаменатель будет равен 0.
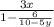
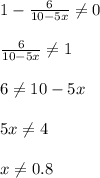
x∈(-∞;0.8)∪(0.8;+∞)
все таки математика настигла огромной волной и накрыла корнями и дробными степенями ???
(x)^1/n = ⁿ√x (например x^1/3 = ∛x x^1/2 = √x)
x² - y² = (x - y)(x + y)
(x + y)² = x² + 2xy + y²
(x^n)^m = x^(nn)
x^n * x^m = x^(n+m)
ⁿ√xⁿ = x (для положительных х)
x^-1 = 1/x
1. 64^1/6 = ⁶√(2⁶) = 2
2. 27 ^2/3 = ∛ 27² = ∛ (3³)² = 3² = 9
3. 0^51/4 = 0 (0 в любой положительной степени = 0)
5. x^1/2 = (x^1/4)²
(a^1/2 - b^1/2) / (a^1/4 + b^1/4) = (a^1/4 - b^1/4)(a^1/4 + b^1/4)/(a^1/4 + b^1/4) = a^1/4 - b^1/4
4. (x^1/3 + y^1/3)² - 2∛(xy) - 1/(∛y)^-2 = x^2/3 + 2x^1/3*y^1/3 + y^2/3 - 2x^1/3*y^1/3 - y^2/3 = x^2/3
^ - степень ( x^2/3 = ∛x² икс в степени две третьих)
(b²-ab) / (a²+ab)= b(b-a) / a(a+b)
Упростим второе выражение:
(а-4)/(b-8)=(a-1)/(b-2)
(a-4)(b-2) =(b-8)(a-1)
ab-2a-4b+8=ab-b-8a+8
ab-2a-4b+8-ab+b+8a-8=0
6a-3b=0
3(2a-b)=0 | :3
2а-b=0
2a=b
подставим значение второго выражения (b=2a) в первое:
2а(2а-а) / а(а+2а) = (2а*а) /(а*3а) = 2а²/ 3а²= 2/3
ответ: 2/3.