см, тогда второй катет - 
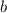см. Площадь прямоугольного треугольника равна 
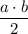, что составляет 210 см² или перепишем сразу 
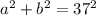
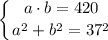
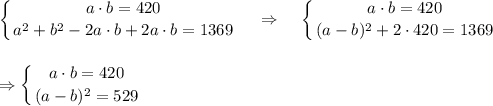
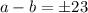. Тогда имеем несколько случаев.
, то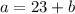 
и подставим в первое уравнение.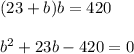
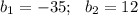см и корень 
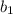не удовлетворяет заданному условию
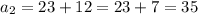см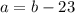
,то подставив в первое уравнение, получим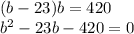
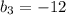
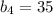см и корень 
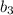не удовлетворяет условию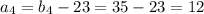
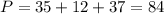см
ответ:
тангенс угла наклона прямой, содержащей диагональ квадрата (в условиях она проходит через данные вершины) = -1/2. угол между сторонами квадрата и диагональю - пи/4. тогда тангенсы углов наклона прямых, содержащих стороны квадрата, равны -3 и 1/3 (соответственные значения получаются применением формулы тангенса суммы к тг (пи - арктг (1/2) - пи/4) и тг (пи - арктг (1/2) + пи/ значит, уравнения прямых принимают вид у = -3х - 1 и у = (1/3)х - 1.
п. с. почему-то символы из раскладки использовать не получается, поэтому функции тангенс и арктангенс обозначены соответственно тг и арктг.
объяснение:
