Відповідь:
a ≥ -1
Пояснення:
Спочатку розв'яжемо подвійну нерівність. Розглянемо два можливих випадки під час розкриття модуля.
Перший: вираз під знаком модуля невід'ємний.
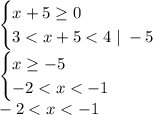
Другий: вираз під знаком модуля від'ємний
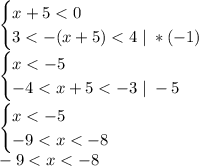
Отже, множина розв'язків цієї нерівності
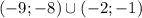
Виразимо x із нерівності з параметром:
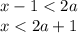
Видно, що всі розв'язки подвійної нерівності менші за -1. Тобто якщо вираз (2a+1) буде не меншим за -1, то він буде більшим і за кожний розв'язок подвійної нерівності. Інакше кажучи, підставивши замість x розв'язок нерівності 3<|x+5|<4 у нерівність x<2a+1, де 2a+1 ≥ -1 (конкретне значення), отримаємо правильне твердження. А це задовольнить умову задачі.
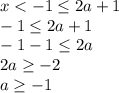
V₁ = π/4
V₂ = 16π
V₃ = 2π
Объяснение:
Высота(H) конуса, его образующая(L) и радиус(R) основания образуют прямоугольный треугольник, причем образующая выступает в полученном треугольнике в роли гипотенузы.
L² = R² + H²
Одновременно, для угла (α) между высотой и образующей:
cosα = R/L
Заменим в формуле Пифагора (L) на (R/cosα = R/0.8 = 5R/4):
(5R/4)² = R² + H²
H = √(25R²/16 - R²) = √(9R² / 16) = 3R/4
Объём конуса (V) равен:
V = 1/3 * S₍осн₎ * H = 1/3 * πR² * H = 1/3 * πR² * 3R/4 = πR³/4
Для данных R₁, R₂, R₃:
1) V₁ = π*1³/4 = π/4
2) V₂ = π*4³/4 = 16π
3) V₃ = π*2³/4 = 2π
Пусть одна сторона равна x, а вторая y,
тогда
2*(x+y)=46 => x+y=23
и
x^2+y^2=(17)^2 => x^2+y^2= 289
из первого уравнения
x=23-y
подставляем во 2-е уравнение
(23-y)^2+y^2=289
529-46y+y^2+y^2=289
2y^2-46y+240=0
y^2-23y+120=0
D=b^2-4ac=49
y1=(23+7)/2=15 => x1=23-y1=8
y1=(23-7)/2=8 => x2=23-y2=15
Стороны равны 8 и 15