Функция убывает при x ∈ [- 2; 0] ; [2; + ∞).
Функция возрастает при x ∈ (- ∞; - 2] ; [0; 2].
Объяснение:
y = - x⁴ + 8x² - 16
y' = - 4x³ + 16x
y' = 0
- 4x³ + 16x = 0
4x(x² - 4) = 0
x = 0, x² - 4 = 0
(x - 2)(x + 2) = 0
x = 2 x = - 2
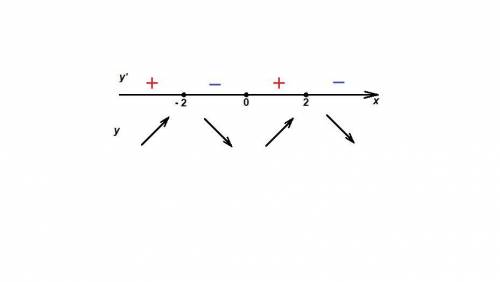
Отметим точки на координатной прямой и определим знаки производной на получившихся интервалах (знаки чередуются, справа минус), см. рисунок.
Если на промежутке производная положительна, то функция возрастает, если отрицательна - убывает.
Функция убывает при x ∈ [- 2; 0] ; [2; + ∞).
Функция возрастает при x ∈ (- ∞; - 2] ; [0; 2].
здесь вероятность того, что в n деталях их 10000 откажут ровно k=2 элемента. β=np=1000*0.002=2 то есть формула применима (β<10) и вероятность 2-х отказов 2²*/2е²=2/е²≈0,27
найдем вероятность 1 отказа 2/2е=1/е≈0,37
искомая вероятность не более 2-х отказов 0,27+0,37=0,64