Объяснение:
Принимаем всю работу за единицу (1). ⇒
Скорость выполнения работы одним мастером равна 1/12.
Скорость выполнения работы тремя мастерами равна 3/12=1/4.
Скорость выполнения работы одним учеником равна 1/30.
Скорость выполнения работы учеников впятером равна 5/30=1/6. ⇒
Скорость выполнения работы, когда работают 3 мастера и 5 учеников
одновременно равна:
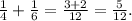
Таким образом, 3 мастера и 5 учеников работая вместе, выполнят работу за: 1:(5/12)=12/5=2,4 (дня).
ответ: 3 мастера и 5 учеников работая вместе,
выполнят работу за 2,4 дня.
ответ: функция непрерывна на всей числовой оси.
Объяснение:
Функция cos(x), а вместе с ней и функция y=3^[cos(x)], определена на всей числовой оси. Мы докажем непрерывность функции в точке x0, где x0 - любая точка числовой оси, если докажем стремление к нулю выражения y(x0+Δx)-y(x0) при Δx⇒0. Но y(x0+Δx)-y(x0)=3^cos(x0+Δx)-3^cos(x0)=3^[cos(x0)*cos(Δx)-sin(x0)*sin(Δx)]-3^cos(x0). При Δx⇒0 cos(Δx)⇒1, а sin(Δx)⇒0, поэтому выражение cos(x0)*cos(Δx)-sin(x0)*sin(Δx) стремится к cos(x0), а выражение 3^[cos(x0)*cos(Δx)-sin(x0)*sin(Δx)]-3^cos(x0) - к нулю. Таким образом доказана непрерывность данной функции на всей числовой оси.
1) 1 • 0,8 = 0,8 ( цены ) после 1-го снижения
2) 0,8 • 0,75 = 0,6 ( цены ) после 2-го снижения
3) 1 - 0,6 = 0,4 = 40 %
ответ на 40 %
N 2
1) 1 • 1,2 = 1,2 ( цены ) после 1-го повышения
2) 1,2 • 1,25 = 1,5 ( цены ) после 2-го повышения
3) 1,5 - 1 = 0,5 = 50 %
ответ на 50 %