
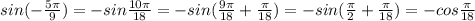
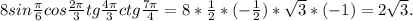
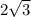
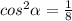
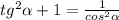

S1=80 cм2
S2=245 см2
Объяснение:
Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Коэффициент подобия k=4/7, но нам неизвестна площадь ни одного треугольника, а известна только сумма площадей S1+S2=325.
Обозначим:
S1 - площадь первого треугольника
325-S1=S2 - площадь второго треугольника
Составим отношение:
S1/(325-S1)=(4/7)^2
Возводим в квадрат дробь справа:
S1/(325-S1)=16/49
По правилу креста:
S1*49=16*(325-S1)
49*S1=5200-16*S1
49*S1+16*S1=5200
65*S1=5200
S1=5200:65
S1=80 cм2
Площадь второго треугольника 325-S1=325-80=245 см2
Видимо, в задании ошибка - пропущены квадраты во вторых слагаемых каждого уравнения.
Условие задания введения новой переменной решите уравнения a) х⁴ - 5х² + 4 = 0 и b) x⁴ - 25x² + 144 = 0.
Нужно знать:
1) уравнение вида ах⁴ + bх² + с = 0 (а ≠ 0) называется биквадратным.
его решения: вводим новую переменную у = х², получаем уравнение ау² + bу + с = 0, решаем полученное квадратное уравнение, находим его корни у₁ и у₂, а затем решаем уравнения х² = у₁ и х² = у₂.
Поэтому:
a) х⁴ - 5х² + 4 = 0,
у = х², у² - 5у + 4 = 0,
D = (-5)² - 4 · 1 · 4 = 25 - 16 = 9; √9 = 3;
у₁ = (5 - 3)/(2 · 1) = 2/2 = 1, у₂ = (5 + 3)/(2 · 1) = 8/2 = 4,
х² = 1 , х = ±1;
х² = 4, х = ±2.
ответ: -2; -1; 1; 2.
b) x⁴ - 25x² + 144 = 0
у = х², у² - 25у + 144 = 0,
D = (-25)² - 4 · 1 · 144 = 625 - 576 = 49; √49 = 7;
у₁ = (25 - 7)/(2 · 1) = 18/2 = 9, у₂ = (25 + 7)/(2 · 1) = 32/2 = 16,
х² = 9 , х = ±3;
х² = 15, х = ±4.
ответ: -4; -3; 3; 4.
sin(-5π/9)=-sin(π-4π/9)-sin4π/9
cos1,8π=cos(2π-0,2π)=cos0,2π
ctg0,9π=ctg(π-0,1π)=-ctg0,1π
a)8sinπ/6*cos2π/3*tg4π/3*ctg7π/4=8*1/2*(-1/2)*(-√3)*(-1)=-2√3
5sin²α+13cos²α=6
5sin²α+13(1-sin²α)=6
5sin²α+13-13sin²α=6
8sin²α=7
sin²α=7/8⇒cos²α=1-7/8=1/8
tg²α=sin²α/cos²α=7/8÷1/8=7
ответ:7.