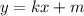: если k>0, функция возрастает, k<0 - убывает. Всё просто. Т.е. в убывании обе функции линейные, k<0 и в первом (k=-7), и во втором 
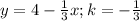. С этим разобрались. Теперь к возрастанию. Я не знаю, в каком Вы классе, постараюсь объяснить доступно. Чтобы определить возрастание/убывание функции, нужно взять значения 
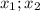, два произвольных числа, но 
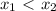. Пусть мы имеем функцию 
, тогда вычисляем значения функции в этих двух точках, имеем 
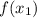и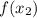 
, так вот, если 
, тогда функция возрастающая, если же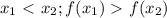 
, то она убывающая, но только ПРИ УСЛОВИИ, что она монотонна на всей области определения (т.е. ТОЛЬКО возрастает или ТОЛЬКО убывает), в противном случае мы говорим о ПРОМЕЖУТКАХ возрастания и убывания. 1)
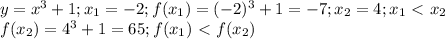, т.е. функция возрастающая. А вот задание с 
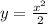не совсем корректно, так как эта функция возрастает только при x>0, при x<0 она убывает, x=0 - Точка экстремума. Если уж брать математический анализ, то легко взять производную и исследовать функцию на "скорость изменения" (алгебраический смысл производной) 
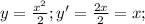. Если производная в некоторой точке отрицательная, то функция убывает, если производная положительная, то функция возрастает, если производная равна 0, то это точка экстремума. Очевидно, что при x<0 функция убывает, при x>0 возрастает. Если же доказывать возрастание на промежутке x>0, тогда действуем, как и в первом случае (только не берем значения из ненужного нам промежутка): 
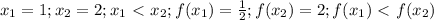, функция возрастает, что и требовалось доказать.
1) б, в, г.
2) в.
3) г.
4) г.
5) б.
Объяснение:
1) Вид прямолинейной функций: Y=KX+B, где К-это угловой коэффициент при Х, а В-это величина смещения прямой относительно центра координат. Графики прямолинейных функций параллельны в том случае, когда угловые коэффициенты К и знак перед К при х совпадают, но при этом различные B. По существу К-это угол наклона между графиком прямой и осью Х. Если угол наклона одинаков, то прямые параллельны.
2) Для нахождения точки пересечения оси Y, нужно X прировнять к 0, и подставить в выражение функций: y=-0,5*0+1=1. Искомая точка (0;1).
3) Если точка принадлежит графику функций, то при подстановке координаты точки Х в выражение функций, значение функций должно совпасть со значением Y координаты точки.
Пример 1: т. D(0;1), у(0)=-0,5*0+1=1, значение функций совпало со значением координаты Y точки D. Следовательно точка D принадлежит графику функций.
Пример 2: т. А(-1;0), у(-1)=-0,5*(-1)+1=1,5, значение функций не совпадает со значением координаты Y точки A. Следовательно точка А не принадлежит графику функций.
4) Чтобы найти точки пересечения двух графиков функций, нужно составить из них систему уравнений. Корни системы уравнений и будут точки пересечения графиков функций. Составим систему:
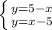
5-x=x-5
-2*x=-10
x=5 - это координата Х точки пересечения. Найдём координату Y подставив х=5 в любое из уравнений:
у=5-х=5-5=0 - это координата Y точки пересечения. Точка пересечения c координатами: (5;0).
5) Если B<0, то график прямолинейной функций ниже начала координат. Если B>0, то график прямолинейной функций выше начала координат. В данном случае он ниже начала координат.
Если К>0, то график расположен в первой и третьей четверти координатной плоскости. Если К<0, то график расположен во второй и четвёртой четверти координатной плоскости.
х+3 км\ч - скорость катера по течению
х-3 км\ч - скорость катера против течения
5(х+3)=7(х-3)
5х+15=7х-21
-2х=-36
х=18 км\ч - собственная скорость катера(скорость катера в стоячей воде)
5(18+3)=5*21=105 км - расстояние между городами