Пусть большее простое число из T(x) равно n.Сравним числа:n^2 и 2T(x),то есть квадрат наибольшего простого числа и удвоенную сумму простых чисел до n:
Очевидно,что все простые числа,кроме 2 нечетные,а значит T(x) меньше суммы двойки и натуральных нечетных чисел от 1 до n(так как не все нечетные числа являются простыми).
Рассмотрим данную сумму,члены которой,кроме двойки образуют арифметическую прогрессию.
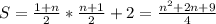
Сравним 2S и n^2
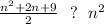


Правая часть больше левой(нуля) при:

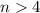
А так как S>T(X) и n^2>2S,то n^2>2T(x)
Значит и x^2>2T(x) при n,указанном выше.
Рассмотрим оставшиеся 2 варианта:
n=2 n=3

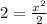


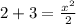
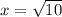
ответ: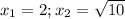
Выиграет первый. Покажем его план действий.
Первым ходом он отодвинет фишку в самый конец, тем самым сходив на 50 клеток. Затем каждый следующий ход он будет возвращать фишку обратно на последнюю клетку. Более того, длины его ходов никогда не повторятся - докажем это. Предположим обратное - пусть он повторит длину хода. Тогда он сходит из места, в которое ранее сходил второй игрок. Однако он сходил туда из позиции 50, то есть он сам повторил длину хода. Противоречие. Итак, так как длина ходов когда нибудь повторится, а это будет не случай первого, то второй проиграет.