ответ: первый насос наполнит бассейн за 10 часов .
Пусть 1 насос наполняет бассейн за х часов, тогда его производительность = 1/х (объёма бассейна в час) .
Пусть 2 насос наполняет бассейн за у часов, тогда его производительность = 1/у (объёма бассейна в час) .
Производительность 1 насоса в 1,5 раза выше производительности 2 насоса, тогда (1/х):(1/у)=1,5 ⇒ (у/х)=1,5 , у=1,5х .
Совместная производительность равна
(1/х)+(1/у)=(1/х)+(1/1,5х)=(2,5/1,5х)=5/(3х) .
Тогда за 6 часов, работая вместе, насосы наполнят 1 бассейн . ⇒
А - объём работы (1 бассейн) , р - производительность , t - время .
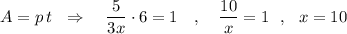
Первый насос наполнит бассейн за 10 часов, а второй за у=1,5*10=15 часов.
вторая производная от формулы пути или первая производная от формулы скорости - это ускорение.
Найдем сначала скорость
v= s '(t) = (t^3 - t) ' = 3t^2 - 1;
Приравняем это значение к 8 (задано в условии) и найдем время t.
3t^2 - 1= 8;
3t^2 = 9;
t^2 = 3;
t = sgrt3(квадратный корень из 3).
Теперь найдем формулу ускорения и подставим в нее значение времени.
a= v '(t) = (3t^2 - 1) ' = 6t;
a(sgrt3) = 6*sgrt3.
ответ 6*квадратный корень из 3.