![+ , - , \cdot , : , x^n , \sqrt[n]{x} и \log_a{x}](/tpl/images/0480/8307/7c93b.png) – имеют ОДНОЗНАЧНЫЙ результат. Вы, возможно знаете пока не все из них, но это не меняет ничего в рассуждениях. Однозначность действия означает, что при вычислении результата любого из них получается однозначный ответ. Ну, например, ведь нет такого, что у одного при вычислении
– имеют ОДНОЗНАЧНЫЙ результат. Вы, возможно знаете пока не все из них, но это не меняет ничего в рассуждениях. Однозначность действия означает, что при вычислении результата любого из них получается однозначный ответ. Ну, например, ведь нет такого, что у одного при вычислении 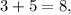 а у другого
а у другого 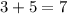 :–) ?! Конечно же, нет, это бы вызывало полную неразбериху и ни в одной науке ничего нельзя было бы вычислить ни по одной формуле. Но иногда, при изучении квадратного корня, учащиеся понимают это действие не совсем корректно, полагая, что
:–) ?! Конечно же, нет, это бы вызывало полную неразбериху и ни в одной науке ничего нельзя было бы вычислить ни по одной формуле. Но иногда, при изучении квадратного корня, учащиеся понимают это действие не совсем корректно, полагая, что 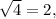 но одновременно с тем как бы и
но одновременно с тем как бы и 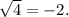 Это ошибка! Так понимать действие корня нельзя. Любой калькулятор покажет именно
Это ошибка! Так понимать действие корня нельзя. Любой калькулятор покажет именно 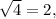 и это и есть верный результат вычислений, поскольку он единственный, так как любое арифметическое действие должно давать ОДНОЗНАЧНЫЙ результат.
и это и есть верный результат вычислений, поскольку он единственный, так как любое арифметическое действие должно давать ОДНОЗНАЧНЫЙ результат.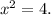 Корни этого нелинейного уравнения, как легко понять:
Корни этого нелинейного уравнения, как легко понять:  и
и 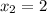 или в короткой записи
или в короткой записи 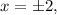 что равносильно
что равносильно 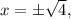 где сам «арифметический квадратный корень»
где сам «арифметический квадратный корень» 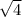 – это именно ПОЛОЖИТЕЛЬНОЕ число, а уж перед ним ставятся разные знаки, чтобы показать, что «корнями этого нелинейного уравнения» являются и само значение «квадратного арифметического корня» и число, противоположное ему. Аналогично, например, для уравнения:
– это именно ПОЛОЖИТЕЛЬНОЕ число, а уж перед ним ставятся разные знаки, чтобы показать, что «корнями этого нелинейного уравнения» являются и само значение «квадратного арифметического корня» и число, противоположное ему. Аналогично, например, для уравнения: 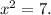 Корни этого нелинейного уравнения, как легко понять:
Корни этого нелинейного уравнения, как легко понять: 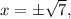 где сам «арифметический квадратный корень»
где сам «арифметический квадратный корень» 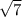 – это именно ПОЛОЖИТЕЛЬНОЕ число, а уж перед ним ставятся разные знаки, чтобы показать, что «корнями этого нелинейного уравнения» являются и само значение «квадратного арифметического корня» и число, противоположное ему.
– это именно ПОЛОЖИТЕЛЬНОЕ число, а уж перед ним ставятся разные знаки, чтобы показать, что «корнями этого нелинейного уравнения» являются и само значение «квадратного арифметического корня» и число, противоположное ему.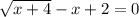 ;
;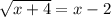 ;
;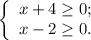
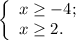
![x \in [ 2 ; +\infty ]](/tpl/images/0480/8307/22de1.png) ;
;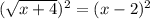 ;
;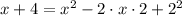 ;
;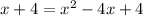 ;
;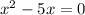 ;
;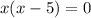 ;
;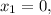 это не соответствует ОДЗ, поскольку
это не соответствует ОДЗ, поскольку ![x_1 = 0 \notin [ 2 ; +\infty ]](/tpl/images/0480/8307/72ba8.png) ;
;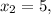 что соответствует ОДЗ, поскольку
что соответствует ОДЗ, поскольку ![x_2 = 5 \in [ 2 ; +\infty ]](/tpl/images/0480/8307/2f42f.png) ;
;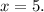
б) 9-х^2y^2=(3-xy)(3+xy)
(x-3y)(x+3y)=x^2-9y,
c^2-d^2/bc-bd=(c-d)(c+d)/b(c-d)=(c+d)/b,
3x^2-27/3x-x^2=3(x^2-9)/x(3-x)=3(x-3)(x+3)/-x(x-3)=3(x+3)/-x=-3(x+3)/x,
а) (x+0,2z)(x^2-0,2xz+0,04z^2)=x^3+0,008z^3 - сумма кубов;
б) (4a-1)(16a^2+4a+1)=64a^3-1 - разность кубов;
а)4x^2-4=4(x^2-1)=4(x-1)(x+1),
б) 5t^2-20st+20s^2=5(t^2-4st+4s^2)=5(t-2s)(t-2s),
в) c(1-27d^3)=c(1-3d)(1+3d+9d^2),
г) v(u^3+w^3)=v(u+w)(u^2-uw+w^2).