Пусть х - число десятков , а у - число единиц в возрасте мужчины. Его возраст (10х + у), а возраст его сына равен (х + у).
Составляем уравнение: (10х + у) + (х + у) = 67
9х + 2(х + у) = 67
х + у = 0,5(67 - 9х) -возраст сына.
Наложим ограничения:
1) х<10
2) х -не должно быть чётным числом, иначе х + у будет нецелым
3) у<10.
Из х + у = 0,5(67 - 9х) получим
у = 0,5(67 - 9х) - х = 0,5((67 - 9х - 2х) = 0,5((67 - 11х)
решим неравенство
0,5((67 - 11х) < 10
67 - 11х < 20
11х > 47
х > 4,27,
С учётом того, что х -целое положительное число, имеем
х > 4
4) х+ у > х - это очевидно, поэтому справедливо неравенство 0,5(67 - 9х) > х
67 - 9х > 2х
11х < 67
х < 6,09
т.е.
х < 6
В границах х∈(4;6) есть только одноцелое число х = 5.
Тогда у = 0,5((67 - 11·5) = 6
И возраст сына х + у = 5 + 6 = 11
Ну, и заодно: возраст отца 56 лет
ответ: сыну 11 лет
Довольно интересная задача, которая наверняка имеет множество решений, постараюсь поподробнее изложить своё.
Итак, возраст отца определяется двузначным числом a1a0, где a1 и a0 - цифры данного числа.
Представим данное число в виде разложения на слагаемые, по формуле перевода чисел в десятичную систему счисления:
a1a0 = a0 * 10^0 + a1 * 10^1 = a0 + 10a1.
Суммарный возраст отца и сына равен 67, запишем это в виде уравнения с двумя неизвестными:
a0 + a1 + a0 + 10a1 = 67
2a0 + 11a1 = 67, мы получили диофантово уравнение, которое требуется решить в натуральных числах, так как возраст - величина положительная.
Решим с использованием следующей системы неравенств:
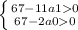
Решая получаем, что a1 < 6, а a0 < 33.
Интервал значений a0 слишком велик, поэтому будет отталкиваться от значений a1.
Теперь дело остаётся за банальным перебором:
Если a1 = 1, то возраст отца равен 128, что невозможно.
Если a1 = 2, то уравнение 2a0 + 11a1 = 67 в решении не нуждается, так как при подстановке получим, что сумма чётных чисел равна числу нечётному, что невозможно. Впредь будем рассматривать только те значения a1, которые не кратны двум.
Если a1 = 3, то возраст отца равен 317, что невозможно.
Значение 4 кратно 2, а значит заранее не подходит.
В итоге мы пришли к единственному оставшемуся значению - это 5, оно и будет решением данного уравнения, проверим это.
2a0 + 55 = 67
2a0 = 12
a0 = 6
Возраст отца равен 56, тогда возраст сына - 11.
Искомый ответ: 11.
7x+3/4=7x-1
7x-7x=-1-3/4
0=-1 3/4 уравнение не имеет решений
2)x^2+5x+1=0
D=25-4=21
x₁=(-5-√21)/2
x₂=(-5+√21)/2
3) 2x-5/3 - 1> 3-x
2x+x>3+1+5/3
3x>4 5/3
3x> 17/3
x>17/9
x∈(17/9; +∞)