4. x = 1 ; 2 ; 3 ; 4
5. x = 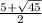 ;
; 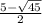 ; 3 ; 2
; 3 ; 2
Объяснение:
4. (x² - 5x)(x² - 5x + 10) + 24 = 0
Произведем замену: (x² - 5x) = t
Тогда: t(t + 10) + 24 = 0
t² + 10t + 24 = 0
D = 10² - 4·24 = 100 - 96 = 4
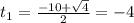 ;
; 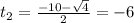
Произведем обратную размену: t = (x² - 5x)
• (x² - 5x) = -4
x² - 5x + 4 = 0
D = (-5)² - 4·4 = 25 - 16 = 9
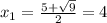 ;
; 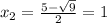
• (x² - 5x) = -6
x² - 5x + 6 = 0
D = (-5)² - 4·6 = 25 - 24 = 1
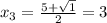 ;
; 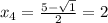
ответ: x = 1 ; 2 ; 3 ; 4
5. (x² - 5x + 2)(x² - 5x - 1) = 28
Произведем замену: x² - 5x = t
(t + 2)(t - 1) = 28
t² - t + 2t - 2 = 28
t² + t - 30 = 0
D = 1² - 4·(-30) = 1 + 120 = 121
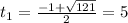 ;
; 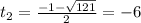
Произведем обратную размену: t = (x² - 5x)
• x² - 5x = 5
x² - 5x - 5 = 0
D = (-5)² - 4·(-5) = 25 + 20 = 45
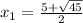 ;
; 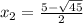
• (x² - 5x) = -6
x² - 5x + 6 = 0
D = (-5)² - 4·6 = 25 - 24 = 1
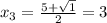 ;
; 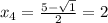
ответ: x = 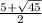 ;
; 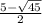 ; 3 ; 2
; 3 ; 2
В общем, у нас есть две прогрессии:
a;a+d;a+2d, и сумма этих членов -9, то есть
a+a+d+a+2d = -9
3a+3d = -9
a+d=-3, заранее выразим d: d=-3-a
вторая прогрессия выглядит так:
a+11;a+d;a+d+1 и она геометрическая, по свойству можем сделать так:
подставим наше выражение:
9=(a+11)(a+2(-3-a)+1)
9 = (a+11)(-a-5)
получим после перемножения уравнение
Ну и находим сумму: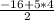 *5=10
*5=10
Итого ответ 10