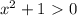при любых действительных значениях x-са, по этому можем на это выражение умножать уравнение ниже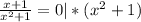
ответ: 453600
Объяснение:
1. Раскрасим основание A1A2...A8 в один из 10 цветов. Такую раскраску можно осуществить
2. Раскрасим теперь по очереди боковые грани пирамиды. Для первой грани SA1A2 имеется 10−1=9 вариантов раскраски, для второй грани SA2A3 имеется 10−2=8 вариантов раскраски, и так далее, для 8-й по порядку грани имеется 10−8=2 вариант(-ов, -a) раскраски. Таким образом, всего получаем
M=10(10−1)(10−2)...(10−8)
вариантов раскраски пирамиды.
3. По условию задачи две раскраски считаются одинаковыми, если получаются друг из друга движением. В нашем случае, у пирамиды существует ровно 8 движений (8 поворотов). Потому искомое число раскрасок будет в 8 раз меньше величины M.
Получаем ответ:
10(10−1)(10−2)...(10−8)8=453600.
ответ: существует ровно 3 числа, удовлетворяющих условию
Объяснение:
Предварительно заметим, что если
n=pv11pv22...pvss — разложение числа n на простые множители, то количество делителей числа n определяется по формуле
d(n)=(v1+1)(v2+1)...(vs+1).
Действительно, любой делитель d числа n имеет вид:
d=pα11pα22...pαss, где 0≤αi≤vi.
Показатель α1 можно выбрать показатель α2 можно выбрать и так далее, показатель αs можно выбрать Таким образом, количество выбрать показатели α1… αs или, что то же самое, выбрать делитель d числа n, которое равно (v1+1)(v2+1)...(vs+1).
1. Пусть n раскладывается на простые следующим образом:
n=3α5βpα11...pαss,
тогда количество делителей n равно
d(n)=(α+1)(β+1)(α1+1)...(αs+1).
2. Разложим исходное число на простые множители:
15=3⋅5.
После умножения n на 15 получим:
15n=3α+15β+1pα11...pαss,
d(15n)=(α+2)(β+2)(α1+1)...(αs+1).
3. Если количество делителей числа 15n увеличилось в 2 раза, то
d(15n)=2d(n) и (α+2)(β+2)(α1+1)...(αs+1)=2(α+1)(β+1)(α1+1)...(αs+1).
Отсюда находим
(α+2)(β+2)=2(α+1)(β+1),
αβ=2.
Таким образом, α=1, β=2 либо α=2, β=1.
Значит, для того чтобы после умножения на 15 количество делителей увеличилось в 2 раза, число должно иметь вид
3152q=75q или 3251p=45p,
где q, p взаимно просты с 15. Отметим, что числа этих видов не пересекаются, так как делятся на разную степень 3.
4. Посчитаем количество чисел указанных видов, не превосходящих 100.
Имеем
75q≤100,
q=1.
Получаем 1 число вида 75q.
Аналогично
45p≤100,
p≤2.
Числа p=1;2 подходят. Получаем 2 варианта чисел вида 45p.
