a) Выражение имеет смысл когда подкоренное выражение неотрицательно. Тогда
-x ≥ 0 ⇔ x ≤ 0 ⇔ x∈(-∞; 0].
b) В силу пункта а) область определения функции : D(y)=(-∞; 0].
Значение квадратного корня неотрицательно, поэтому множество значений функции : E(y)=[0; +∞).
Чтобы построить график функции определим несколько значений функции:
График функции в приложенном рисунке 1.
c) Чтобы показать на графике значения х при у=2 и y=2,5 сначала определим эти значения. Для этого решаем уравнения:
Получили целое число.
Приближенные значение х=–6,25≈–6.
y(наиб) = 31 (в точке х = 2)
y(наим) = 5 (в точке x = 1)
На границах интервала.
Объяснение:
Для того, чтобы найти наибольшее и наименьшее значение функции нам необходимо:
Найти все стационарные точки.
Найти все критические точки.
Проверить границы интервала.
Пункт 1 - стационарные точки:Данные точки ищутся с производной. Найдем производную данной функции:
x'(t) = 8 - 4.
Приравниваем производную к 0:
8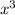
- 4 = 0
t = ±![\sqrt[3]{\frac{4}{3}}](/tpl/images/1201/1296/6cbb5.png)
= ±![\sqrt[3]{\frac{1}{2}}](/tpl/images/1201/1296/97e2a.png)
- однако, эти точки не входят в наш интервал.
Таковых у нас нет, т.к. критические точки - это стационарные точки, но которые не входят в ОДЗ. (У нас ОДЗ от (-∞;∞+)).
Пункт 3 - границы графика:Подставляем значения границ интервала и находим значения в этих точках:
x(1)=2*1^4−4*1+7 = 5
x(2)=2*2^4−4*2+7 = 31
Следовательно, это и есть наибольшее и наименьшее значение функции на заданном интервале.
Строим у=х²-2х=(х-1)²-1
Парабола у=х²,ветви вверх,вершина (1;-1),х=1-ось симметрии,
точки пересечения с осями: (0;0);(2;0)
х=0
у=0
у=0 х(х-2)=0⇒х=0 и х=2
Оставляем то что выше оси ох,а то что ниже отображаем на верх