Одна из сторона прямоугольника равна а см, а другая на 2 см меньше. найдите площадь этого прямоугольника. запишите три последовательных числа, кратных 4, если большее из них равно 4к + запишите общий вид натурального числа, которое при делении на 7 дает в остатке 5.

👇

Увидеть ответ

Ответ:

DmitriyWayne557

07.02.2020

S прямоугольник равна 2а+2в. пусть а см одна сторона,тогда другая сторона а-2 составим уравнение.
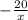
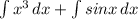
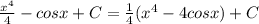
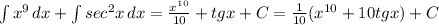
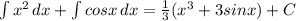
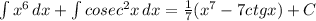
2а+2(а-2)= 2а+2а-4=-4

4,6(79 оценок)

Открыть все ответы

Ответ:

Olesya11111111111111

07.02.2020

1) 1/3 + 5/6 = 2/6 + 5/6 = 7/6 = одна целая 1/6 (общий знаменатель 6)
2) 7/16 × 8/35 = 1/10 (7 сокращается с 35, 8 сокращается с 16)
3) 46/75 ÷ 23/45 = 46/75 × 45/23 = 6/5 = одна целая 1/5 = 1,2 (Переворачиваем вторую дробь и умножаем эти дроби. 46 сокращается с 23, 75 сокращается с 45)
4) 10 ÷ 5/11 = 10 × 11/5 = 22 ( Переворачиваем вторую дробь и умножаем эти дроби. 10 сокращается с 5)
5) 6 - 1 целая 3/5 = 4 целых 2/5(тут все просто, объяснять думаю не надо)
6) 8 целых 3/4 × 1 целая 3/14 = 35/4 × 17/14 = 595 / 56 (думаю ты где то допустил ошибку, когда переписывал)

4,8(81 оценок)

Ответ:

anastasia69smirnova

07.02.2020

1.-4cos(x)+C(тут и подробно ну нужно, ибо тупо по формуле ну и -4 за знак интеграла)
2. $\int{-9 sec^2x} \, dx =-9 \int{sec^2x} \, dx = -9 tgx+C$
представил 1/cosx как secx
3.6sinx (аналогично первому)
4. ну тут аналогично второму, сначала представим 1/sinx, как cosecx и получим:
$\int {-16cosec^2x} \, dx =-16 \int {cosec^2x} \, dx = 16ctgx+C$
5. $\frac{3}{2} \int { \sqrt{x} } \, dx =\frac{3}{2}* \frac{2x^ \frac{3}{2} }{3} =x^ \frac{3}{2}+C$
6. аналогично по формуле,-15 выносим за знак интеграла, 1/x^2=-1/x,
получаем -15*(-1/x)=15/x+C
7. выносим 5/2 за знак интеграла и раскрываем интеграл, используя формулу:
получаем: $\frac{5x^ \frac{3}{2} }{3} +C$ \
8. устал одно и тоже писать, выносим -20 за знак интеграла, применяем формулу и получаем: $- \frac{20}{x}$
9. разобьем на два интеграла: $\int{x^3} \, dx + \int{sinx} \, dx$
применим формулы для двух интегралов и получим:
$\frac{x^4}{4}-cosx+C= \frac{1}{4}(x^4-4cosx)+C$
10. опять же, представим 1/cosx=secx, затем разобьем на два интеграла и получим:
$\int{x^9} \, dx + \int{sec^2x} \, dx= \frac{x^{10}}{10}+tgx+C= \frac{1}{10} (x^{10}+10tgx)+C$
11. эхх, устал...
$\int {x^2} \, dx + \int {cosx} \, dx = \frac{1}{3}(x^3+3sinx)+C$
12. аналогично десятому.
представляем 1/sinx=cosec x, разбиваем на два интеграла и используем формулы, получаем:
$\int {x^6} \, dx + \int {cosec^2 x} \, dx= \frac{1}{7}(x^7-7ctgx)+C$