Радиус вписанной в многоугольник окружности равен отношению его площади к полупериметру
r=S:p, где р - полупериметр
Треугольник тоже многоугольник, и радиус вписанной в него окружности найдем по этой формуле.
Чтобы найти площадь треугольника, нужно знать его третью сторону, основание.
Высота известна, боковая сторона - тоже.
Высота делит равнобедренный треугольник на два равных прямоугольных, в которых боковая сторона - гипотенуза. высота и половина основания - катеты..
Найдем половину основания по т.Пифагора:
0,5а=√(225-144)=9 см
Основание равно 2*9=18 см
Площадь треугольника
S=ah:2=18*12:2=108 см²
полупериметр
р=(18+30):2=24
r=108:24=4,5 см
Треугольник равнобедренный. Для вписанной в равнобедренный треугольник окружности, когда известны все стороны и высота, можно вывести формулу:
r=0,5*bh:0,5(2a+b)
или произведение высоты на основание, деленное на периметр.
r=bh:Р
r=18*12:(30+18)=4,5
Объяснение:
а) 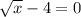 а)
а) 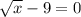
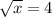
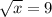
х=16 х=81
б) 1/3х²=3 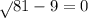
х²=9 х=81
х1=-3 б) 1/2х²=2
х2=3 х²=4
в) -4х²=1/4 х1=-2 х2=2
4х²=-1/4 в) -5х²=1/5
Рівняння не має розв*язків 5х²=-1/5 рівняння розвязків не має
г) -2х²+2,42=0 г) -3х²+2,43=0
-2х²=121/50=0 -3х²+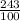 = 0
= 0
-100х²+121=0 -300х²+243=0
-100х²=-121 -300х²=-243
х²=121/100 х²=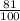
х1=-1,1 х1=-0,9, х2=0,9
х2=1,1